
The length and width of a rectangle are in ratio of 3:4. If the rectangle has an area of
A. 15 cm
B. 12 cm
C. 25 m
D. 25 cm
Answer
495.9k+ views
Hint: We will first find the length and width of the rectangle by using the given ratio and area of the rectangle. Let the length of rectangle is
Complete step-by-step answer:
Let the common ratio of length and width of rectangle be
Then, the length of rectangle is
We know that the area of the rectangle is
Then, the area of the given rectangle is
But, we are given that the area of the rectangle is
Divide both sides by 12
Take square root on both sides,
Therefore, the length of the rectangle is
We have to find the length of the diagonal of the rectangle.
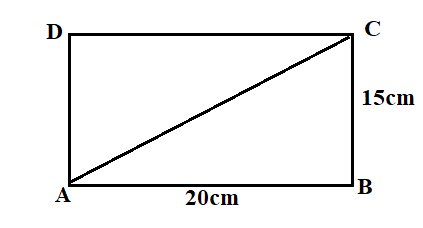
In a rectangle all angles are right angles.
Therefore,
We want to find the length
We will use Pythagoras theorem to find the value of
Hence,
On substituting the values of
After taking square root on both sides, we will get,
Also, the diagonals of the rectangle are equal.
Hence, the value of the rectangle is 25 cm
Thus, option D is correct.
Note: One should know the basic properties of a rectangle, such as all the angles of a rectangle are equal to
Complete step-by-step answer:
Let the common ratio of length and width of rectangle be
Then, the length of rectangle is
We know that the area of the rectangle is
Then, the area of the given rectangle is
But, we are given that the area of the rectangle is
Divide both sides by 12
Take square root on both sides,
Therefore, the length of the rectangle is
We have to find the length of the diagonal of the rectangle.

In a rectangle all angles are right angles.
Therefore,
We want to find the length
We will use Pythagoras theorem to find the value of
Hence,
On substituting the values of
After taking square root on both sides, we will get,
Also, the diagonals of the rectangle are equal.
Hence, the value of the rectangle is 25 cm
Thus, option D is correct.
Note: One should know the basic properties of a rectangle, such as all the angles of a rectangle are equal to
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Whom did king Ashoka send to Sri Lanka to spread Buddhism class 7 social science CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

How many crores make 10 million class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

Find HCF and LCM of 120 and 144 by using Fundamental class 7 maths CBSE





