Question

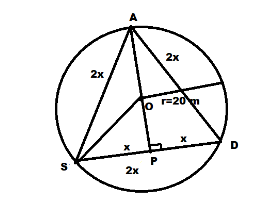
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in their hands to talk to each other. Find the length of the string of each phone.

Answer 1

Hint: Here we will first assume the distance between each of the two boys to be 2x. Here we will do a construction which is we will draw a perpendicular from A and then apply Pythagoras theorem in each of the triangles so formed and finally find the value of x.

Complete step-by-step answer:
Let the distance between each of the two boys be 2x.
Now since the distance between each of the two boys is equal, therefore, ASD is an equilateral triangle.
Now, we have drawn \[OP \bot SD\]
Therefore, \[SP = PD = \dfrac{1}{2}SD\]
Putting the value we get,
\[SP = PD = \dfrac{1}{2}2x\]
\[ \Rightarrow SP = PD = x\]
Now in \[\Delta OPS\]
Applying Pythagoras theorem we get:-
\[O{S^2} = O{P^2} + P{S^2}\]
Putting in the values we get:-
\[{\left( {20} \right)^2} = O{P^2} + {x^2}\]
Simplifying it further we get:-
\[O{P^2} = 400 - {x^2}\]
Taking the square root we get:-
\[\sqrt {O{P^2}} = \sqrt {400 - {x^2}} \]
\[ \Rightarrow OP = \sqrt {400 - {x^2}} \]
Now in \[\Delta APS\]
Applying Pythagoras theorem we get:-
\[A{S^2} = A{P^2} + P{S^2}\]
Putting in the values we get:-
\[{\left( {2x} \right)^2} = A{P^2} + {x^2}\]
Simplifying it we get:-
\[4{x^2} = A{P^2} + {x^2}\]
\[ \Rightarrow A{P^2} = 3{x^2}\]
Taking square root both the sides we get:-
\[\sqrt {A{P^2}} = \sqrt {3{x^2}} \]
\[AP = \sqrt 3 x\]
Now we know that,
\[AP = OA + OP\]
Putting in the respective values we get:-
\[\sqrt 3 x = 20 + \sqrt {400 - {x^2}} \]
\[ \Rightarrow \sqrt 3 x - 20 = \sqrt {400 - {x^2}} \]
Now squaring both the sides we get:-
\[{\left( {\sqrt 3 x - 20} \right)^2} = {\left( {\sqrt {400 - {x^2}} } \right)^2}\]
Applying the following identity:-
\[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
We get:-
\[{\left( {\sqrt 3 x} \right)^2} + {\left( {20} \right)^2} - 2\left( {\sqrt 3 x} \right)\left( {20} \right) = 400 - {x^2}\]
Simplifying it further:-
\[3{x^2} + 400 - 40\sqrt 3 x = 400 - {x^2}\]
Simplifying it further we get:-
\[4{x^2} = 40\sqrt 3 x\]
Solving for x we get:-
\[4x = 40\sqrt 3 \]
\[ \Rightarrow x = 10\sqrt 3 \]m
Therefore, the distance between each of the two boys is:-
\[AS = SD = AD = 2\left( {10\sqrt 3 } \right)\]
\[ \Rightarrow AS = SD = AD = 20\sqrt 3 m\]

Therefore, the length of the string is \[20\sqrt 3 m\]

Note: Students might forget to multiply the value of x obtained by 2 which may lead to wrong answers.
Also, since it is given that all the boys are seated in equal distance from each other that is why the length of the string would be the same for each boy.
According to Pythagoras theorem, in a right angled triangle, the sum of squares of perpendicular and base is equal to the square of hypotenuse of the triangle.
\[{\left( {hypotenuse} \right)^2} = {\left( {perpendicular} \right)^2} + {\left( {base} \right)^2}\]