Question

A closed box measures 66cm, 36cm and 21cm from outside. If its walls are made of metal sheet 0.5cm thick then find the weight of the box, if 1\[c{m^3}\]of metal weighs 3.6g
A. 17985.6g
B. 15725.6g
C. 13625.6g
D. 15825.6g

Answer 1

Hint: Here we draw a diagram of a box having length breadth and height as given in the question. Use the formula for volume of a cuboid to obtain the volume of the box from outside. Subtract the value of thickness from each measurement to obtain measurements from the inside of the box. Calculate the volume from inside of the box using volume of a cuboid. Subtract the volume of the box from inside from the volume of the box from outside. Using a unitary method find the weight of the box.
* Volume of a cuboid having length\[l\], breadth\[b\]and height\[h\]is given by \[l \times b \times h\].
* Unitary method helps us to find the value of multiple units when we are given the value of a single unit by multiplying the number of units to the value of a single unit.

Complete step-by-step answer:
We draw a diagram of a box in cuboid shape having length 66cm, breadth 36cm and height 21cm.

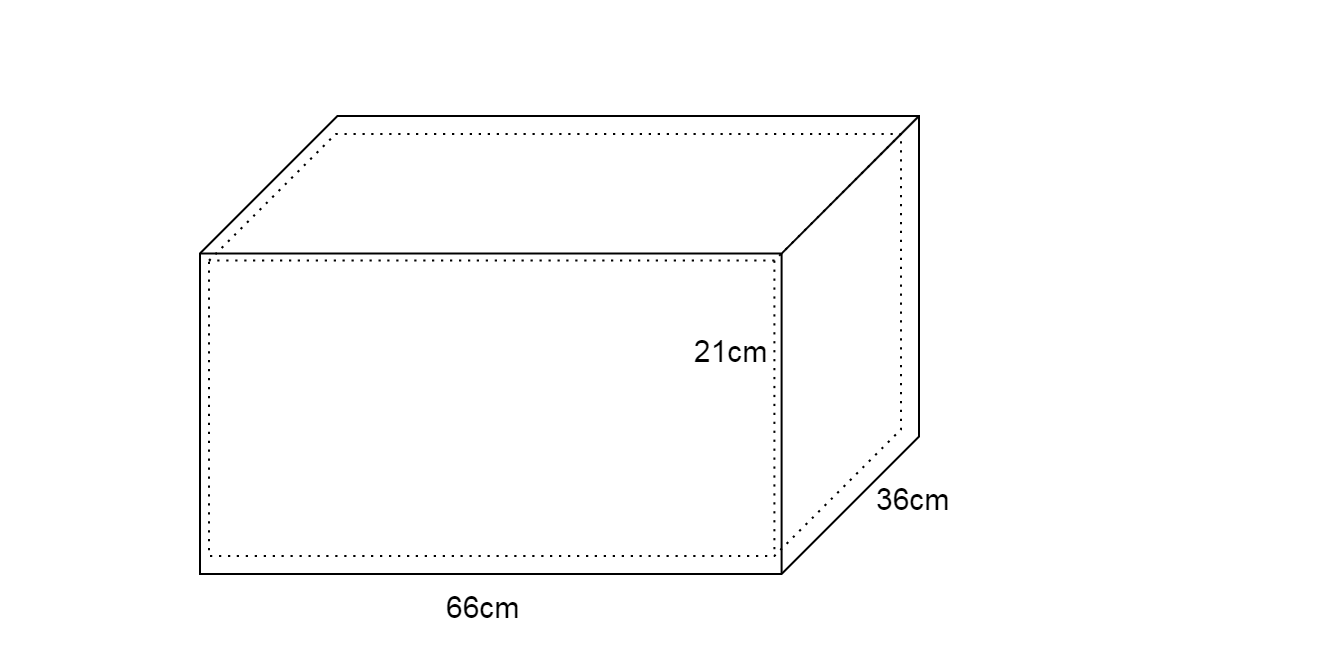
We have \[l = 66,b = 36,h = 21\].
Formula for volume of a cuboid is \[V = l \times b \times h\]
Substitute the values in the formula
\[ \Rightarrow V = 66 \times 36 \times 21\]
\[ \Rightarrow V = 49,896\]\[c{m^3}\] … (1)
Now we know the thickness of the metal walls is 0.5cm and the walls are on both all sides of the box. So each face is reduced by 0.5cm thickness two times. To understand this better we can draw a diagram stating the thickness.

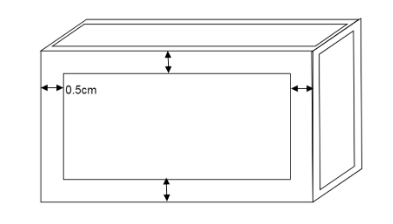
Therefore we reduce the value \[2 \times 0.5 = 1\]cm from all measurements to obtain the measurements of the inside of the box.
Let length, breadth and height from the inside of the box be denoted by \[l',b',h'\]respectively.
Then
\[l' = l - 1\]
Substitute the value of l as 66
\[ \Rightarrow l' = 66 - 1 = 65\]cm
\[b' = b - 1\]
Substitute the value of b as 36
\[ \Rightarrow b' = 36 - 1 = 35\]cm
\[h' = h - 1\]
Substitute the value of h as 21
\[ \Rightarrow h' = 21 - 1 = 20\]cm
Then the volume of the box from inside is \[V' = l' \times b' \times h'\]
\[ \Rightarrow V' = 65 \times 35 \times 20\]
\[ \Rightarrow V' = 45,500\]\[c{m^3}\] … (2)
Now we find the volume of the metal sheet by subtracting the volume of box from inside from the volume of box from outside.
Volume of metal sheet \[ = V - V'\]
Substitute the values of volumes from equation (1) and (2)
\[ \Rightarrow \]Volume of metal sheet \[ = 49,896 - 45,500\]\[c{m^3}\]
\[ \Rightarrow \]Volume of metal sheet \[ = 4396\]\[c{m^3}\]
Now we are given if 1 \[c{m^3}\]of metal weighs 3.6g
Use unitary method to find the weight of 4396 \[c{m^3}\]of metal
Weight of if 1 \[c{m^3}\]of metal \[ = 3.6\]g
Weight of if 4396 \[c{m^3}\]of metal \[ = 3.6 \times 4396\]g
\[ \Rightarrow \]Weight of if 4396 \[c{m^3}\] of metal \[ = 15825.6\]g

So, option D is correct.

Note: Students might make the mistake of subtracting only the value 0.5cm of thickness when finding the measurements from inside of the box. Keep in mind thickness is of each wall and so the box is reduced in measurement from each side.