A concave mirror is half dipped in water. Focal length of the portion of mirror in the air is $f_{1}$ and focal length of the mirror in water is $f_{2}$ . Then (Take refractive index of water = 4/3)
A. $f_{1} > f_{2}$
B. $f_{1} < f_{2}$
C. $f_{1} = f_{2}$
D. $f_{1} \geq \frac{4}{3} f_{2}$

Answer

Verified

480k+ views

Hint: The focal length of a mirror is a constant quantity. It does not change with medium nor does it depend on the refractive index of a medium. Hence, the focal length of the mirror in air is equal to the focal length of the mirror in the water.

Complete answer:
The distance from the centre of the mirror to the focal point is the focal length. Focal point for a concave mirror is the point on the optical axis on which light rays that are initially parallel to the optical axis converge after they reflect off the mirror. Now, since focal length is a distance, it is a constant quantity. It will not vary depending upon the medium. Hence, focal length of the concave mirror in air will be equal to the focal length of the concave mirror in water, that is,

f_{1} = f_{2}

. Refractive index of a medium is defined as the ratio between speed of sound in vacuum to the speed of sound in that medium. The focal length of the concave mirror in water does not depend on this value. A diagram can be illustrated as follows:

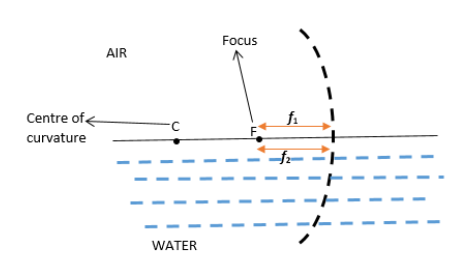
The answer is option C.

Note:
The apparent depth of the mirror in water may appear less than the real depth when observed from air due to refraction of light. But this will not change the focal length of the mirror in any case. The focal length of the mirror is half of the radius of curvature. Since, the radius of curvature remains constant irrespective of the medium, focal length will also remain constant.