Question

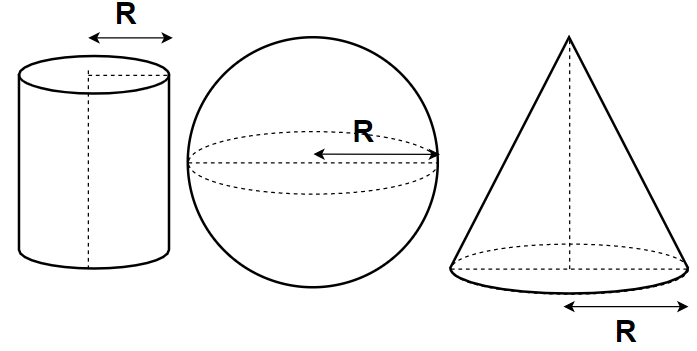
A cone, a hemisphere and a cylinder stand on equal bases of radius R and have the same heights H. The whole surface area in the ratio ?

A. $(\sqrt{3}+1):3:4$
B. $(\sqrt{2}+1):7:8$
C. $(\sqrt{2}+1):3:4$
D. none of these

Answer 1

Hint: In this problem we will use the equation as the radius and height of the hemisphere are equal to each other, so we can measure the total surface area of a cone, a hemisphere and a cylinder separately and eventually find the ratio.

Complete step by step answer:
Since the argument that a circle, a globe, and a cylinder stand on equal R-radius bases and have the same H-heights.
Here it can be observed that the radius and height of a hemisphere are equal,
so, $R=H-(1)$
This means that the circle, hemisphere and ring are equal in height and radius.
Now we'll measure the total cone, hemisphere and cylinder surface area
Height of slant= $\sqrt{H^2+R^2}=\sqrt{2}R$
As we know the total cone surface area is given as =
 $\pi R(L+R)=\pi R(\sqrt{2R}+R)=(\sqrt{2}+1)\pi R^2$
For hemisphere , total surface area is given as $3\pi R^2$
From equation 1 we will substitute the value of H
$2\pi R(R+H)=2\pi R(2R)=4\pi R^2$

Now for cylinder, total surface area is given as
$4\pi R^2$
Now we will calculate the ratio, so we get
Total surface area of cone : total surface area of hemisphere : total surface area of cylinder
$$$(\sqrt{2}+1)\pi R^2:3\pi R^2:4\pi R^2$
By solving it we get
$(\sqrt{2}+1):3:4$
Hence the correct answer is option C.
Note:
A cone is a three-dimensional geometric shape that smoothly tapers from a flat base to a point called the apex or vertex. A cylinder has historically been a three-dimensional solid, one of the most fundamental of curvilinear geometric shapes.