Question

A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the remaining solid after the cone is carved out.

Answer 1

Hint: The radius of the cone will be half of the length of the side of the cube and the height of the cone will be equal to the length of the side of the cube. Subtract the total surface area of the cone from the total surface area of the cube to find the remaining area.

Complete step by step answer:
It is given that the cone of maximum size is carved out of the cube. Maximum size refers to the maximum volume of the cone that fits in the cube. Such a cone should have a diameter and height equal to the length of the side of the cube. Now, to find the area of the remaining solid, we must imagine how the solid will look when we remove the cone.
Let us assume that the length of the side of the cube is $a=14\text{ cm}$. Therefore, height of the cone $=h=14\text{ cm }$ and radius of the cone $=\dfrac{14}{2}=7\text{ cm}$. Let the slant height of the cone be $'l'$. Therefore, using Pythagoras theorem: $l=\sqrt{{{r}^{2}}+{{h}^{2}}}$.
When the cone is removed then we will be able to see a hollow cone from the base of the cube. Only the lateral surface area of the cone will be present because the circular base of the cone has been removed.

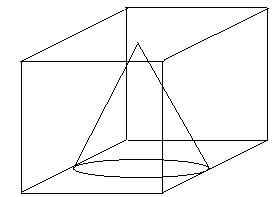
Therefore, the remaining surface area of the solid will be:
$\begin{align}
  & \text{=lateral surface area of cone}+\text{total surface area of cube}-\text{area of base of cone} \\
 & \text{=}\pi rl+6{{a}^{2}}-\pi {{r}^{2}} \\
 & =\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}+6{{a}^{2}}-\pi {{r}^{2}} \\
 & =\dfrac{22}{7}\times 7\times \sqrt{{{7}^{2}}+{{14}^{2}}}+6\times {{14}^{2}}-\dfrac{22}{7}\times {{7}^{2}} \\
 & =\dfrac{22}{7}\times 7\times 7\sqrt{5}+6\times {{14}^{2}}-\dfrac{22}{7}\times {{7}^{2}} \\
 & =154\sqrt{5}+1176-154 \\
 & =344.96+1176-154 \\
 & =1366.96\text{ c}{{\text{m}}^{2}} \\
\end{align}$
Hence, the surface area of the remaining solid is $1366.96\text{ c}{{\text{m}}^{2}}$.

Note: Since, the cone is a right circular cone that means height, slant height and radius of the cone will form a right angle triangle with slant height as its hypotenuse and we know that $hypotenuse=\sqrt{perpendicula{{r}^{2}}+bas{{e}^{2}}}$. This formula is used to determine the slant height. Also, we have used the value of $\pi =\dfrac{22}{7}$ to minimize the calculation. $\sqrt{5}=2.27$ is used.