
A cone whose height is equal to the diameter, is increasing in volume at the rate of
(A)
(B)
(C)
(D)
Answer
462.3k+ views
Hint: We know that the formulae for finding the volume of the cone given as
Complete step-by-step solution:
Now considering from the question we have been asked to find the increasing rate of radius using the given information in the question which is stated as follows “A cone, whose height is equal to the diameter, is increasing in volume at the rate of
From the basic concepts we know that the formula for finding the volume of the cone given as
As given the height of the cone is equal to its diameter which is mathematically given as
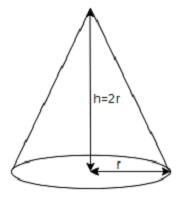
Now we will substitute this value in the formulae then we will have
Now we will differentiate this expression as we need to find the rate at which the radius is increasing for that we will use the formulae given as
In the question it is given that the volume of the cone is increasing at the rate of
By using this we will have
The area of the circular base is given as
By substituting this value we will have
As we know that
Therefore we can conclude that for a cone whose height is equal to the diameter, is increasing in volume at the rate of
Note: While answering questions of this type we should be sure with the calculations and concepts that we apply while answering. The unit conversions should be done carefully. If we had not made the unit conversions then we will have the answer completely vary from the answer. We should also not make mistakes in taking the diameter = two times the radius if we take wrong our whole solution will be wrong.
Complete step-by-step solution:
Now considering from the question we have been asked to find the increasing rate of radius using the given information in the question which is stated as follows “A cone, whose height is equal to the diameter, is increasing in volume at the rate of
From the basic concepts we know that the formula for finding the volume of the cone given as
As given the height of the cone is equal to its diameter which is mathematically given as

Now we will substitute this value in the formulae then we will have
Now we will differentiate this expression as we need to find the rate at which the radius is increasing for that we will use the formulae given as
In the question it is given that the volume of the cone is increasing at the rate of
By using this we will have
The area of the circular base is given as
By substituting this value we will have
As we know that
Therefore we can conclude that for a cone whose height is equal to the diameter, is increasing in volume at the rate of
Note: While answering questions of this type we should be sure with the calculations and concepts that we apply while answering. The unit conversions should be done carefully. If we had not made the unit conversions then we will have the answer completely vary from the answer. We should also not make mistakes in taking the diameter = two times the radius if we take wrong our whole solution will be wrong.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




