Question

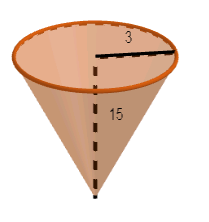
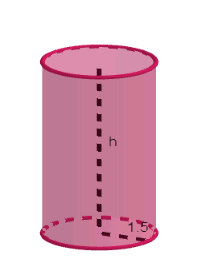
A conical flask is full of water. The flask has base-radius 3 cm and height of 15 cm. The water is poured into a cylindrical glass tube of uniform inner radius of 1.5 cm, placed vertically and closed at the lower end. Find the height of water in the glass tube.
(a) 20 cm
(b) 30 cm
(c) 40 cm
(d) 25 cm

Answer 1

Hint: In this question, we first need to calculate the water in the conical flask using the formula \[\dfrac{1}{3}\pi {{r}^{2}}h\]. Then equate it to the volume of the cylinder which is given by the formula \[\pi {{r}^{2}}h\] taking the height of the cylinder as unknown. Now, on simplifying it further we get the height of the cylinder.

Complete step-by-step answer:
RIGHT CIRCULAR CONE:
A right circular cone is a solid generated by revolving of a right angled triangle through one of its sides containing the right angle as axis.
Volume of a right circular cone is given by the formula
\[\dfrac{1}{3}\pi {{r}^{2}}h\]
RIGHT CIRCULAR CYLINDER:
A right circular cylinder is considered as a solid generated by revolution of a rectangle about one of its side
Volume of a right circular cylinder is given by the formula
\[\pi {{r}^{2}}h\]
Let us assume the volume of the conical flask as v and volume of the cylinder as V
Now, in the question given that radius is 3 cm and height is 15 cm of the conical flask
Now, on comparing these with the values in the formula we get,
\[r=3,h=15\]

Now, from the volume of the cone formula we have
\[\Rightarrow v=\dfrac{1}{3}\pi {{r}^{2}}h\]
Now, on substituting the respective values we get,
\[\Rightarrow v=\dfrac{1}{3}\pi \times {{3}^{2}}\times 15\]
Now, on simplifying this further we get,
\[\therefore v=45\pi \]
Now, let us assume that the height of the cylinder as h
Here, given that radius of the cylinder is 1.5 cm
\[r=1.5\]

Now, from the volume of the cylinder formula we have
\[\Rightarrow V=\pi {{r}^{2}}h\]
Now, on substituting the respective values we get,
\[\Rightarrow V=\pi {{1.5}^{2}}h\]
Now, as water in conical flask is being poured into cylinder we have
\[\Rightarrow V=v\]
Now, on substituting the respective values we get,
\[\Rightarrow \pi {{1.5}^{2}}h=45\pi \]
Now, on cancelling the common terms on both the sides we get,
\[\Rightarrow {{1.5}^{2}}\times h=45\]
Now, on rearranging the terms we get,
\[\Rightarrow h=\dfrac{45}{{{1.5}^{2}}}\]
Now, on further simplification we get,
\[\therefore h=20cm\]
Hence, the correct option is (a).

Note: Instead of calculating the volumes of conical flask and cylinder separately and then equating it we can also simplify this by first considering that the volumes are equal and then substituting the respective values and simplifying further which also gives the same result.It is important to note that as the water is being poured from the conical flask to cylinder the volume remains the same. so, if we consider any other parameters like area to be equal then we get a completely incorrect result.