Question

A container of large uniform cross-section area $A$ resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities $d$ and $2d$, each of height $\dfrac{H}{2}$. The lower density liquid is open to the atmosphere having pressure ${P_0}$.
A homogeneous solid cylinder of length $L$ $\left( {L < \dfrac{H}{2}} \right)$ and cross-section area $\dfrac{A}{5}$ is immersed such that, it floats with its axis vertical at the liquid-liquid interface with length $\dfrac{L}{4}$ in the denser liquid. Determine:
A. The density D of the solid.
B. The total pressure at the bottom of the container.

Answer 1

Hint: To calculate the density D of the solid, apply the Archimedes principle which states that the buoyant force on a body whether fully or partially immersed in a liquid is equal to the weight of the fluid displaced by the body.
The pressure at the bottom of a container due to any liquid is $P = \rho gh$.
Where, $\rho $ and $h$ are the density and height of the liquid. $g = 9.8m.{s^{ - 2}}$.


Complete step by step answer:
Let’s draw the diagram which depicts the question.

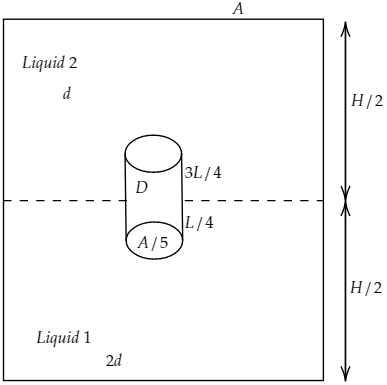
It is given that the uniform cross-section area of the large container is $A$.
The large container rests on a horizontal surface and contains two immiscible, non-viscous and incompressible liquid 1 and liquid 2.
Liquid 1 and 2 have the densities $2d$ and $d$ respectively. The lower density liquid 2 is open to the atmosphere having pressure ${P_0}$.
The length and cross-section area of the given homogeneous solid cylinder are $L$ $\left( {L < \dfrac{H}{4}} \right)$ and $\dfrac{A}{5}$ respectively.
The homogeneous solid cylinder is immersed in such a way that it floats with its axis vertical at the liquid-liquid interface with length $\dfrac{L}{4}$ in the liquid 1 and $\dfrac{{3L}}{4}$ in liquid 2.
Density $\left( D \right)$ of the solid:
Volume of the solid cylinder $V = \dfrac{A}{5} \cdot L$
Mass of the solid cylinder $m = V \times D$
$ \Rightarrow m = \dfrac{{A \times L \times D}}{5}$
Weight of the solid cylinder ${F_s} = mg$
$ \Rightarrow {F_s} = \dfrac{1}{5} \times A \times L \times D \times g$
The buoyant force on the solid cylinder${F_b} = $ Total weight of the fluid displaced by the solid cylinder
${F_b} = $ weight of liquid 1 displaced $ + $ weight of liquid 2 displaced
weight of liquid 1 displaced $ = $ (Partial volume of the solid immersed in the liquid 1)$ \times $ (density of the liquid 1) $ \times $ $g$
So, weight of liquid 1 displaced $ = \left( {\dfrac{L}{4} \times \dfrac{A}{5}} \right) \times 2d \times g$
And weight of liquid 2 displaced $ = \left( {\dfrac{{3L}}{4} \times \dfrac{A}{5}} \right) \times d \times g$
The buoyant force becomes,
${F_b} = \left( {\dfrac{L}{4} \times \dfrac{A}{5} \times 2d \times g} \right) + \left( {\dfrac{{3L}}{4} \times \dfrac{A}{5} \times d \times g} \right)$
Further simplifying
${F_b} = \dfrac{1}{4} \times L \times A \times d \times g$
Since ${F_w} = {F_b}$
$\dfrac{1}{5} \times A \times L \times D \times g = \dfrac{1}{4} \times L \times A \times d \times g$
Further simplifying
$D = \dfrac{5}{4}d$
Hence, the density of the solid cylinder is $\dfrac{5}{4}d$.
The total pressure at the bottom of the container.
The total pressure at the bottom of the container is given by
$P = {P_{atmosphere}} + {P_{liquid1}} + {P_{liquid2}} + {P_{buoance}}$
It is given that the pressure due to atmosphere ${P_{atmosphere}} = {P_0}$
The pressure due to liquid 1 ${P_{liquid1}} = \dfrac{H}{2} \times 2d \times g$
The pressure due to liquid 2 ${P_{liquid2}} = \dfrac{H}{2} \times d \times g$
Pressure due to buoyance force ${P_{buoance}} = $ (Force on solid cylinder)/(cross-section area of the container)
${P_{buoance}} = \dfrac{{\dfrac{A}{5} \times L \times D \times g}}{A}$
$ \Rightarrow {P_{buoyancy}} = \dfrac{1}{5} \times L \times D \times g$
Substitute the required values in the above total pressure formula
$P = {P_o} + \left( {\dfrac{H}{2} \times 2d \times g} \right) + \left( {\dfrac{H}{2} \times 2d \times g} \right) + \left( {\dfrac{1}{5} \times L \times D \times g} \right)$
Further substitute $D = \dfrac{5}{4}d$ and then simplifying
$P = {P_0} + \left( {\dfrac{{3H}}{2} + \dfrac{L}{4}} \right)dg$
Hence the total pressure on the bottom of the container is ${P_0} + \left( {\dfrac{{3H}}{2} + \dfrac{L}{4}} \right)dg$.

Note:The buoyant force is a force exerted on the body immersed in a liquid. So, the buoyant force is an upward force which opposes the weight of an immersed body.
While calculating the total pressure, the pressure due to buoyancy must be considered.