Question

A convex lens A of focal length 20cm and a concave lens G of focal length 5cm are kept along the same axis with the distance between them. If a parallel beam of light falling on A Leaves B as a parallel beam, then the distance d in cm will be
A. 25
B. 15
C. 30
D. 50

Answer 1

Hint: Here we use the concept of the power of the combination of the lens which is the algebraic sum of individual lenses. When two lenses are used in combination, the image is formed by the first lens that then serves as an object for the second lens.

Complete step by step answer:
According to the sign convention, the data are given as,
$ \Rightarrow {f_1} = 20\;cm$
$ \Rightarrow {f_2} = - 5\;cm$
We can refer to the below figure for a proper explanation of the answer.
In the given question we have two lenses one is convex and another one is concave, the convex lens converges here and the concave lens shows divergence. Here the parallel beam of light converges at the focus.

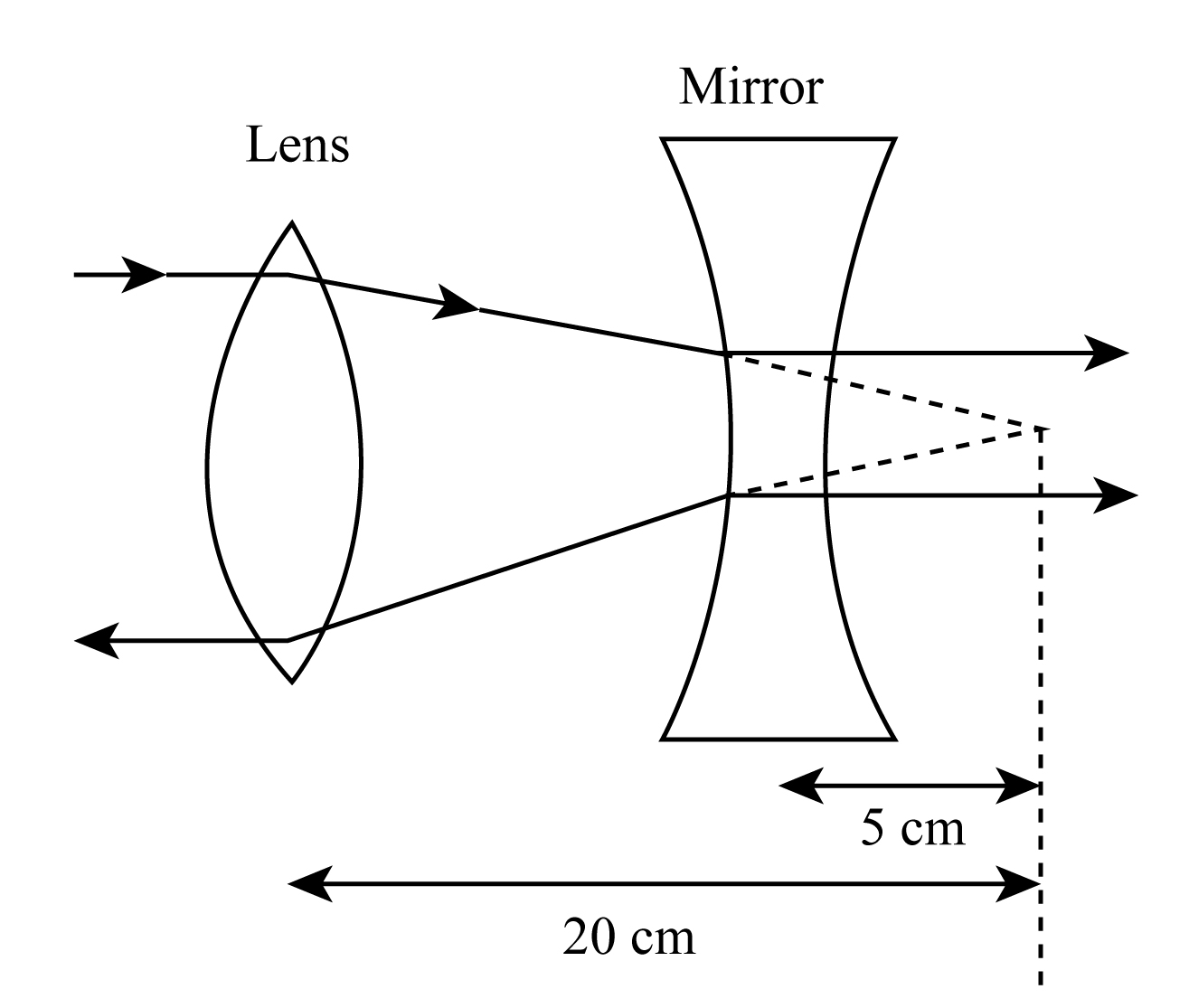
Since the effective focal length of two lenses combination is directly proportional to two lenses placed at a distance d apart.
Therefore, the focal length of combination is given by the formula
$\dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} - \dfrac{d}{{{f_1}{f_2}}}$
Here $f_1$, $f_2$ are the focal lengths and d is the distance and f is the combined focal length.
Since the resultant ray is parallel to the axis, the real image is going to be formed at infinite and hence the combined focal length $f = \infty $
We will now substitute, $f = \infty $ , ${f_1} = 20\;cm$, ${f_2} = - 5\;cm$ to find the value of d.
$\dfrac{1}{\infty } = \dfrac{1}{{20}} + \dfrac{1}{{\left( { - 5} \right)}} - \dfrac{d}{{\left( {20} \right)\left( { - 5} \right)}}$
$\therefore d{\rm{ }} = {\rm{ }} + 15cm$

If a parallel beam of light falling on A leaves B as a parallel beam, then the distance is 15cm. Hence, option (B) is correct.

Note:
Two lenses produce zero power also if the lens is converging with focal length then the power is positive. If another lens is diverging with the focal length then the power becomes negative, therefore the combination of two lenses will be zero.