
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of curvature 20 cm. The two are kept at 15cm apart from each other. A point object lies 60 cm in front of the convex lens. Draw a ray diagram to show the formation of the image by the combination. Determine the nature and position of the image formed.
Answer
509.4k+ views
Hint: Proceed in a step by step manner. First, determine the image formed by the convex lens. Then, use that image as the object for the convex lens. Follow the path of the light beam to determine which formula you have to choose.
Formula used:
For convex lens, the formula is,
For convex mirror, the formula is,
Where, v is the distance of the image from the pole,
u is the distance of the object from the pole,
f is the focal length of the mirror/lens.
Complete step by step answer:
The ray diagram is given below,
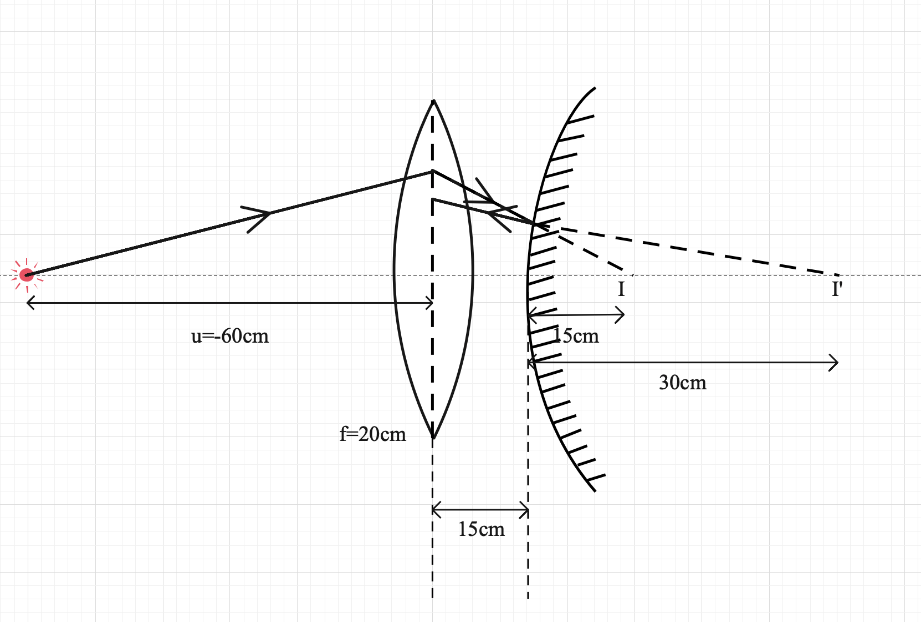
It is very evident from the ray diagram that the image is real.
To determine the position of the final image let us analyze the convex lens and convex mirror one by one.
We need to follow the ray and calculate the position of the image after each refraction.
(i)Convex lens -
Here we need to follow a specific sign convention.
Any distance on the left is considered to be negative and right is considered to be positive.
In this case, u = - 60 cm
Focal length of convex lens is positive. So, f = 20 cm
Putting these values in equation (1) we get,
So, the image due to the convex lens is formed at a distance of 30cm on the right of the lens.
However, there is a convex mirror at a distance of 15 cm from the lens.
So, the imaginary image will be (30-15) = 15 cm towards the right of the convex mirror.
(ii)Convex Mirror -
Now the imaginary object is 15cm on the right of the convex mirror.
So, u = 15 cm
Focal length of the convex mirror is positive. So,
Now, putting these values in equation (2) we get,
Hence the final image is formed at a distance of 30 cm on the right from the pole of the convex mirror. The image is a real virtual.
Note:
You need to be very careful about the sign convention of the object, image, and focal length. The left side of the pole is negative and the right side of the pole is positive. Remember this convection to avoid any mistakes in the future.
The solution only uses the general lens and mirror equations, we can replace the lens and mirror with other variants and get the final result. For example, if we replace the convex lens with a concave lens, the formula remains the same. We just need to consider that the concave lens has negative focal length.
Formula used:
For convex lens, the formula is,
For convex mirror, the formula is,
Where, v is the distance of the image from the pole,
u is the distance of the object from the pole,
f is the focal length of the mirror/lens.
Complete step by step answer:
The ray diagram is given below,

It is very evident from the ray diagram that the image is real.
To determine the position of the final image let us analyze the convex lens and convex mirror one by one.
We need to follow the ray and calculate the position of the image after each refraction.
(i)Convex lens -
Here we need to follow a specific sign convention.
Any distance on the left is considered to be negative and right is considered to be positive.
In this case, u = - 60 cm
Focal length of convex lens is positive. So, f = 20 cm
Putting these values in equation (1) we get,
So, the image due to the convex lens is formed at a distance of 30cm on the right of the lens.
However, there is a convex mirror at a distance of 15 cm from the lens.
So, the imaginary image will be (30-15) = 15 cm towards the right of the convex mirror.
(ii)Convex Mirror -
Now the imaginary object is 15cm on the right of the convex mirror.
So, u = 15 cm
Focal length of the convex mirror is positive. So,
Now, putting these values in equation (2) we get,
Hence the final image is formed at a distance of 30 cm on the right from the pole of the convex mirror. The image is a real virtual.
Note:
You need to be very careful about the sign convention of the object, image, and focal length. The left side of the pole is negative and the right side of the pole is positive. Remember this convection to avoid any mistakes in the future.
The solution only uses the general lens and mirror equations, we can replace the lens and mirror with other variants and get the final result. For example, if we replace the convex lens with a concave lens, the formula remains the same. We just need to consider that the concave lens has negative focal length.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




