Question

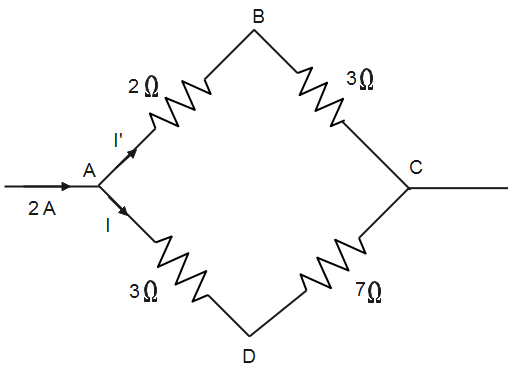
A current of 2A flows in the circuit as shown in the figure. The potential difference ${{V}_{B}}-{{V}_{D}}$ is
(A). $-\dfrac{2}{3}V$
(B). $\dfrac{2}{3}V$
(C). $-\dfrac{4}{3}V$
(D). $\dfrac{4}{3}V$

Answer 1

Hint: The current in the circuit gets divided in the two arms according to the resistance in them as by ohm’s law, resistance is inversely proportional to the current. Applying Kirchhoff’s current law, we can calculate the current in each arm. The potential difference between the points B and D is equal to the sum of potential drops between them.

Formula used:
$I+I'=2$

Complete step-by-step solution:
The Kirchhoff’s voltage law states that the sum of all the potential differences in a loop is zero. It follows the law of conservation of energy.
The Kirchhoff’s current law, the sum of incoming charges and the outgoing charges at a junction is equal to zero. It also follows the law of conservation of charge.
According to Kirchhoff’s current law, from the above figure,
$I+I'=2$ - (1)
Applying loop in ABCDA, we get,
$\begin{align}
  & -2I'-3I'+7I+3I=0 \\
 & \Rightarrow -5I'+10I=0 \\
 & \Rightarrow 10I=5I' \\
\end{align}$
$\Rightarrow I'=2I$ - (2)
Using eq (1) and eq (2), we solve the equation as-
$\begin{align}
  & I+I'=2 \\
 & \Rightarrow I+2I=2 \\
 & \Rightarrow 3I=2 \\
 & \therefore I=\dfrac{2}{3}A \\
\end{align}$
The value of $I$ is $\dfrac{2}{3}A$. Substituting this value in eq (2) we get,
$I'=\dfrac{4}{3}A$
Now, the potential difference between the point B and D will be the sum of all potential drops between the points. Therefore,
$\begin{align}
  & {{V}_{B}}-3I'+7I={{V}_{D}} \\
 & \Rightarrow {{V}_{B}}-3\times \dfrac{4}{3}+7\times \dfrac{2}{3}={{V}_{D}} \\
 & \Rightarrow \dfrac{-12+14}{3}={{V}_{D}}-{{V}_{B}} \\
 & \Rightarrow \dfrac{2}{3}={{V}_{D}}-{{V}_{B}} \\
 & \therefore {{V}_{B}}-{{V}_{D}}=-\dfrac{2}{3}V \\
\end{align}$
The potential difference between the points is $-\dfrac{2}{3}V$.
Therefore, the potential difference ${{V}_{B}}-{{V}_{D}}$ is $-\dfrac{2}{3}V$. Hence, the correct option is (B).

Note: In parallel, the voltage is the same therefore, by the ohm’s law; the current in each parallel arm is inversely proportional to the total resistance in that arm. The points B and D will be at same potential if the resistances are in a constant ratio. The potential difference is negative if the initial point is at higher potential and the final point is at lower potential.