Question

A cylinder, a cone and a hemisphere are of the same base and of same height. Find the ratio of their volumes.

Answer 1

Hint:- We had to only write the formula of volume of cylinder, cone and hemisphere with same height and radius and then divide them to get the ratio of their volumes.

Complete step-by-step answer:

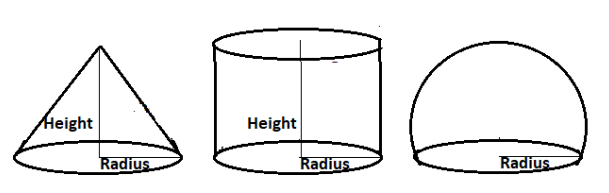
As the height and radius of cylinder, cone and hemisphere are the same.
So, let their height be h units.
And their radius is r units.
Now as we know that the height of the hemisphere is the radius of the hemisphere.
So, r = h (because h is the height of all shapes and r is the radius of all shapes)
So, as we know that if h is the height and r is the radius of cylinder then its volume is calculated as \[\pi {r^2}h\]
Let the volume of the cylinder is \[{V_1}\].
So, \[{V_1} = \pi {r^2}h = \pi {r^3}\] (because h = r)
As we know that if h is the height and r is the radius of cone then its volume is calculated as \[\dfrac{1}{3}\pi {r^2}h\]
Let the volume of the cone is \[{V_2}\].
So, \[{V_2} = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {r^3}\] (because h = r)
As we know that if r is the radius of hemisphere then its volume is calculated as \[\dfrac{2}{3}\pi {r^3}\]
Let the volume of the hemisphere is \[{V_3}\].
So, \[{V_3} = \dfrac{2}{3}\pi {r^3}h\]
Now the ratio of the volumes of cylinder, cone and hemisphere is the ratio of \[{V_1}\], \[{V_2}\] and \[{V_3}\].
So, \[{V_1}:{V_2}:{V_3} = \pi {r^3}:\dfrac{1}{3}\pi {r^3}:\dfrac{2}{3}\pi {r^3} = 1:\dfrac{1}{3}:\dfrac{2}{3}\]
On multiplying ratio be 3. We get,
\[{V_1}:{V_2}:{V_3} = 3:1:2\]
Hence, the volume of the cylinder cone and hemisphere are in ratio 3 : 1 : 2.

Note:- Whenever we come up with this type of problem the first, we had to write the formula of all the given shapes using same parameters and the we check whether any parameter is missing in any formula like here in the formula of volume of hemisphere, height is not present but we know that the height of the hemisphere is same as its radius. So, we had to replace height with radius in the formula of volume of all given shapes because they all had the same height and radius. And after that we can easily divide their volume to get the required ratio of their volumes.