Question

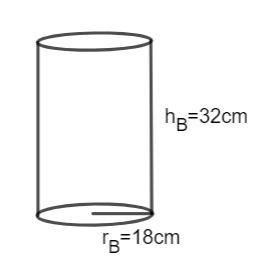
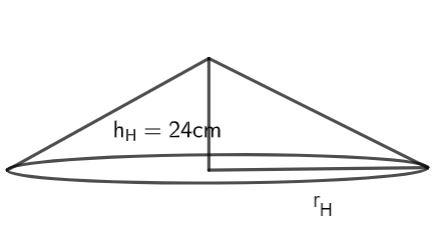
A cylindrical bucket, 32 cm high and with a radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.

Answer 1

Hint: The volume of the sand when it is emptied from the bucket to the ground remains the same. Hence, equate the volume of the cylinder to the volume of the cone to find the radius and the slant height of the heap.

Complete step-by-step answer:

It is given that the sand in the cylindrical bucket is emptied to form a conical heap.
We know that the volume of the sand remains the same.
Hence, the volume of the cylindrical bucket is equal to the volume of the conical heap.
The volume of a cylindrical bucket is given as follows:
\[{V_B} = \pi {r_B}^2{h_B}\]
The height of the cylindrical bucket is 32 cm and the radius is 18 cm. Then, we have:
\[{V_B} = \pi {(18)^2} \times 32..........(1)\]
The volume of the conical heap is given as follows:
\[{V_H} = \dfrac{1}{3}\pi {r_H}^2{h_H}\]
We know that the height of the conical heap is 24 cm, hence, we have:
\[{V_H} = \dfrac{1}{3}\pi {r_H}^2 \times 24\]
\[{V_H} = 8\pi {r_H}^2...........(2)\]
Equating equation (1) and equation (2), we get:
\[32\pi {(18)^2} = 8\pi {r_H}^2\]
Solving for \[{r_H}\], we get:
\[{r_H}^2 = \dfrac{{32\pi {{(18)}^2}}}{{8\pi }}\]
Canceling \[\pi \], we have:
\[{r_H}^2 = \dfrac{{32{{(18)}^2}}}{8}\]
Dividing 32 by 8, we get 4, which is square of 2.
\[{r_H}^2 = 4{(18)^2}\]
\[{r_H}^2 = {(2)^2}{(18)^2}\]
 Taking square root on both sides, we get:
\[{r_H} = 2 \times 18\]
\[{r_H} = 36cm\]
Hence, the radius of the conical heap is 36 cm.
We know that the slant height of the cone is given as follows:
\[l = \sqrt {{r^2} + {h^2}} \]
Then, we have:
\[{l_H} = \sqrt {{{(36)}^2} + {{(24)}^2}} \]
\[{l_H} = \sqrt {1872} \]
\[{l_H} = \sqrt {1872} \]
\[{l_H} = \sqrt {12 \times 12 \times 13} \]
\[{l_H} = 12\sqrt {13} cm\]
Hence, the value of the slant height is \[12\sqrt {13} \] cm.

Note: Remember, the volume of the sand remains the same and since the cylindrical bucket was filled with sand and then emptied to form a conical heap, the two volumes are the same. When taking the square root, take only the positive root, since the radius is a positive quantity.