Question

A cylindrical tennis ball container can contain a maximum three-ball stacked on one another. The top and bottom balls also touch the lid and the base of the container respectively. If the volume of a tennis ball is $240c{{m}^{3}}$, then what is the volume of the container?
(a) $1080c{{m}^{3}}$
(b) $840c{{m}^{3}}$
(c) $1440c{{m}^{3}}$
(d) $720c{{m}^{3}}$

Answer 1

Hint: The approach we will be taking to solve the problem that, we will find the radius of the individual tennis ball. We have been given the volume of a tennis ball. The volume of a sphere is ${{V}_{sphere}}=\dfrac{4}{3}\pi {{r}^{3}}$ . Then, we can show the height of the container in terms of the radius and finally find the volume of the container. The volume of the cylinder is given by ${{V}_{cylinder}}=\pi {{r}^{2}}h$ .

Complete step-by-step answer:
To understand the problem in a better way we need to draw the diagram and try to interpret,

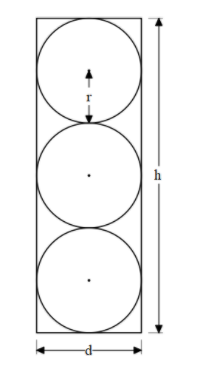
The above diagram is the side view of the above problem.
In this, the tennis balls are touching the container in all directions.
The immediate interpretation that we can make is the radius of the container and the radius of the tennis ball is the same.
Therefore, the radius of the tennis ball, as well as the container, be $r$ .
The volume of the tennis ball is given as $240c{{m}^{3}}$ .
The volume of the sphere is $V=\dfrac{4}{3}\pi {{r}^{3}}...................(i)$
Substituting the values of the Volume we get,
$240=\dfrac{4}{3}\pi {{r}^{3}}$ ,
Solving further we get,
$\pi {{r}^{3}}=240\times \dfrac{3}{4}=180...................(ii)$
We are not substituting the values of $\pi $ because to make the calculation simpler.
As we can see in the diagram that three balls are stacked one above another.
Let us consider the height of the container to be $h$ .
Therefore, according to the condition we get,
$\begin{align}
  & 3\times 2\times r=h \\
 & h=6r.................(iii) \\
\end{align}$
As we need to find the volume of container which is shaped as cylinder the formula is as follows,
The volume of the container $=\pi {{r}^{2}}h$ .
Substituting the value of $h$ we get,
The volume of the container $=\pi {{r}^{2}}\left( 6r \right)=6\pi {{r}^{3}}$ ,
Substituting the value of $\pi {{r}^{\text{3}}}$ from equation (ii) we get,
Volume of container $=6\times \left( 180 \right)=1080c{{m}^{3}}$ .
Therefore, the volume of the container is $1080c{{m}^{3}}$ .
Hence, the correct option is (a).

Note: To make the calculation easier we did not substitute the value of $\pi $ and we did not calculate the value of $r$ individually to avoid the decimal calculation. Instead, we substituted the value of $\pi {{r}^{3}}$ which makes the calculation much easier. Such tricks help in not making calculation mistakes and can be practised. Also, the volume of a single tennis ball is given, it is easily mistaken as the combined volume of all tennis balls.