Answer
336k+ views
Hint: A solid can exist in two forms i.e., as a crystalline solid and as an amorphous solid. In crystalline solids, the components have regular ordered arrays and are held together by uniform intermolecular forces whereas the atoms in amorphous solids are not arranged in a regular array. The atoms in a crystalline solid are arranged in a regular repeating three-dimensional array known as crystal lattice.
Complete answer: Crystal lattice: It is defined as the geometrical and symmetrical three-dimensional arrangement of atoms, ions or components inside a crystalline solid as points.
Characteristics of a crystal lattice:
1.The crystal is made up of many atoms which are represented as points in a lattice and hence known as lattice points in a crystal lattice.
2.On combining the lattice points, the shape of a crystal can be determined.
3.There exists a total fourteen Bravais lattices and all have unique shapes and properties.
A crystal lattice is further divided into seven systems which are as follows:
In a simple hexagonal system, the structure consists of four axes in which three axes are of the same length and are present on the same plane. The fourth axis intersects the other three axes at the right angle. The structure of hexagonal crystal system is represented as follows:
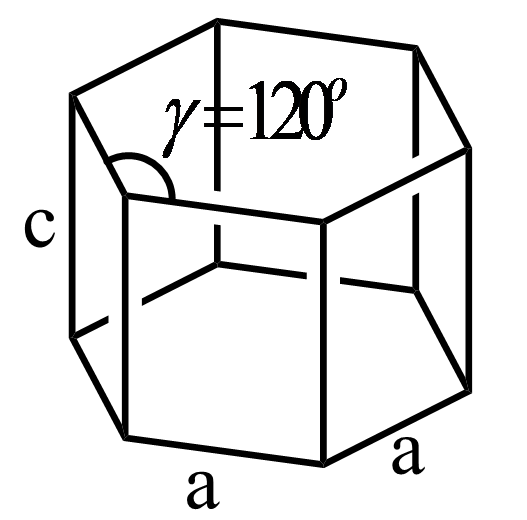
Hence, the relation between the angles $\alpha $, $\beta $ and $\gamma $ in simple hexagonal crystal is as follows:
\[\alpha = \beta = {90^o}\,\,\,\gamma = {120^o}\]
Note:
A crystal system can be described in fourteen different three-dimensional configurations known as Bravais lattice. It is an array of distinct points with an orientation and arrangement which look similar from any distinct point. In the hexagonal crystal system, only one type of Bravais lattice is possible i.e., simple hexagonal cell.
Complete answer: Crystal lattice: It is defined as the geometrical and symmetrical three-dimensional arrangement of atoms, ions or components inside a crystalline solid as points.
Characteristics of a crystal lattice:
1.The crystal is made up of many atoms which are represented as points in a lattice and hence known as lattice points in a crystal lattice.
2.On combining the lattice points, the shape of a crystal can be determined.
3.There exists a total fourteen Bravais lattices and all have unique shapes and properties.
A crystal lattice is further divided into seven systems which are as follows:
| Crystal system | Edge length | Angles |
| Cubic | $a = b = c$ | $\alpha = \beta = \gamma = {90^o}$ |
| Tetragonal | $a = b \ne c$ | $\alpha = \beta = \gamma = {90^o}$ |
| Orthorhombic | $a \ne b \ne c$ | $\alpha = \beta = \gamma = {90^o}$ |
| Monoclinic | $a \ne b \ne c$ | $\alpha = \beta = {90^o}$$\gamma \ne {90^o}$ |
| Hexagonal | $a = b \ne c$ | $\alpha = \beta = {90^o}$$\gamma = {120^o}$ |
| Rhombohedral | $a = b = c$ | $\alpha \ne \beta \ne \gamma \ne {90^o}$ |
| Triclinic | $a \ne b \ne c$ | $\alpha \ne \beta \ne \gamma \ne {90^o}$ |
In a simple hexagonal system, the structure consists of four axes in which three axes are of the same length and are present on the same plane. The fourth axis intersects the other three axes at the right angle. The structure of hexagonal crystal system is represented as follows:

Hence, the relation between the angles $\alpha $, $\beta $ and $\gamma $ in simple hexagonal crystal is as follows:
\[\alpha = \beta = {90^o}\,\,\,\gamma = {120^o}\]
Note:
A crystal system can be described in fourteen different three-dimensional configurations known as Bravais lattice. It is an array of distinct points with an orientation and arrangement which look similar from any distinct point. In the hexagonal crystal system, only one type of Bravais lattice is possible i.e., simple hexagonal cell.
Recently Updated Pages
An indicator HIn has a standard ionization constant class 11 chemistry CBSE

An Indian philosopher who said that the smallest particles class 11 chemistry CBSE

An increase in temperature in a liquid would cause class 11 chemistry CBSE

An increase in equivalent conductance of a strong electrolyte class 11 chemistry CBSE

An increase in both atomic and ionic radii with atomic class 11 chemistry CBSE

An impure sample of sodium oxalate Na2C2O4 weighing class 11 chemistry CBSE

Trending doubts
Which of the following is the most stable ecosystem class 12 biology CBSE

Which are the Top 10 Largest Countries of the World?

Difference Between Plant Cell and Animal Cell

Which of the following is the most stable ecosystem class 12 biology CBSE

Write an application to the principal requesting five class 10 english CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Write a letter to the principal requesting him to grant class 10 english CBSE

The term vaccine was introduced by A Jenner B Koch class 12 biology CBSE



