Question

(a) Define electric flux. Is it a scalar or a vector quantity?
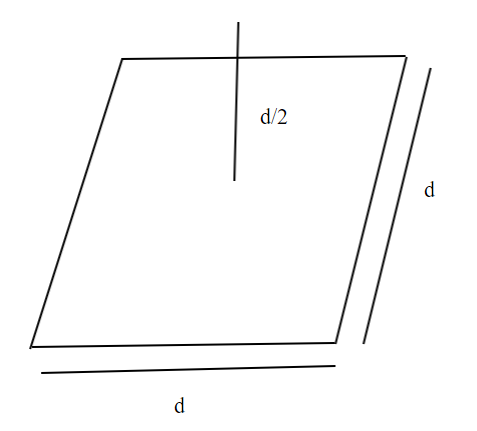
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss’ law to obtain the expression for the electric flux through the square.

(b) If the point charge is now moved to a distance ‘d’ from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.

Answer 1

- Hint: First, we will write the definition of electric flux. With the help of the definition, we will solve the given problem, using the Gauss law \[\phi {\text{ = }}\dfrac{{\text{q}}}{{{\varepsilon _0}}}\]. We will use the symmetry to solve the given problem.

Complete step-by-step solution -

Now, electric flux is a number of electric lines of forces which passes through any cross – sectional area when the cross – sectional area is kept perpendicular to the direction of electric field. It is represented by $\phi $. It is a dot product of electric field vector (vector E) and area vector (vector ds).
Therefore, flux $\phi {\text{ = E}}{\text{.ds}}$
As it is a dot product. So, electric flux is a scalar quantity.
Now, Gauss law states that electric flux through any closed surface is equal to the net charge enclosed inside the surface divided by the permittivity of vacuum.
So, \[\phi {\text{ = }}\dfrac{{\text{q}}}{{{\varepsilon _0}}}\], where q is the net charge enclosed inside the surface.
Now, we are given a charge placed at a distance of d/2 above the square of side ‘d’. Let us suppose a cube of side ‘d’ enclosing a charge q. So, one of its square sides is shown in the figure.
Now, as all the sides of the cube are equal to each other. So, let the flux passing through one side be x. As there are 6 sides in a cube. So, total flux passing through the sides of the cube = 6x.
Now, according to Gauss law, we know that total flux \[\phi {\text{ = }}\dfrac{{\text{q}}}{{{\varepsilon _0}}}\]. But, total flux = 6x.
So, we get \[{\text{6x = }}\dfrac{{\text{q}}}{{{\varepsilon _0}}}\]
x = $\dfrac{{\text{q}}}{{6{\varepsilon _0}}}$
so, flux from one side of the cube is $\dfrac{{\text{q}}}{{6{\varepsilon _0}}}$. So, flux through the shown figure is $\dfrac{{\text{q}}}{{6{\varepsilon _0}}}$.

(b) Now, the charge is placed at a distance d from the centre of square. Also, the side of the square is 2d in this case. Again, assuming a cube of side 2d having charge q at the centre of the cube, where x is the flux passing from one side, we have total flux = 6x.
Therefore, by Gauss law, \[{\text{6x = }}\dfrac{{\text{q}}}{{{\varepsilon _0}}}\]
x = $\dfrac{{\text{q}}}{{6{\varepsilon _0}}}$
So, flux from one side of the cube is $\dfrac{{\text{q}}}{{6{\varepsilon _0}}}$. So, there is no change in the electric flux.

Note: When we come up with such types of questions, we will follow a few steps to solve the given problem. First, we will write the formula we require to solve the problem. Then, we will use the symmetry if in case it is required. After it, we will apply the formula carefully to find the solution. When we use the Gauss law, which is \[\phi {\text{ = }}\dfrac{{\text{q}}}{{{\varepsilon _0}}}\], q is the total charge enclosed in the object. Charge other than q is not considered to find the flux passing through an object.