Question

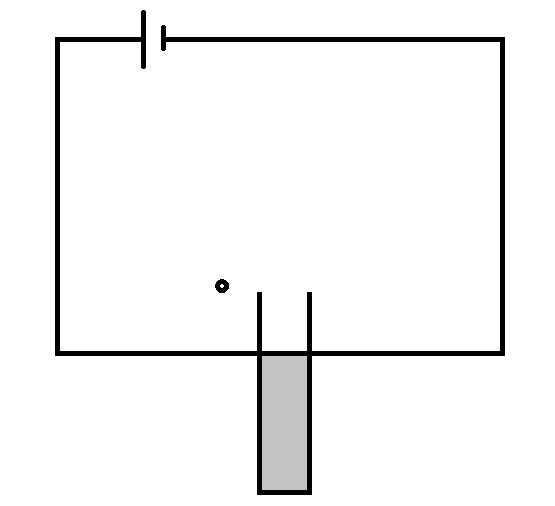
A dielectric slab of dielectric constant $ k $ , mass $ m $ , thickness $ d $ , and area $ L \times L $ is hanging vertically in equilibrium under the influence of gravity and electrostatic pull of a capacitor connected to a battery of voltage $ V $ . The capacitor has plates of area $ L \times L $ and distance between plates is $ d $ . The capacitor is half-filled by the dielectric. Suddenly a mass of $ m $ is attached to the dielectric without any impulse on the system. The slab falls off in time $ t $ . Evaluate $ t $ (in a sec). Take $ k = 2 $ , $ V = 4volts $ , $ L = 80cm $ , $ d = 0.1mm $ .

Answer 1

Hint: We will first evaluate the new capacitance after the dielectric is inserted in it. Then using that capacitance we will evaluate the electrostatic pull due to the battery and using these parameters and given quantities we will evaluate the time the slab falls off when some mass is introduced without any impulse.

Formula used:
The formula of the capacitance
 $ \Rightarrow C = \dfrac{{k{E_0}xL}}{d} $
Electrostatic potential energy formula
 $ \Rightarrow U = \dfrac{1}{2}{C_{new}}{V^2} $
Electrostatic force
 $ \Rightarrow {F_E} = - \dfrac{{dU}}{{dx}} $ .

Complete step by step solution:
Suppose at any point $ x $ , the length $ L $ of the dielectric is inserted between the capacitor $ C $ .
Hence the new capacitance will be given as
 $ \Rightarrow {C_{new}} = {C_1} + {C_2} $
 $ \Rightarrow {C_{new}} = \dfrac{{{E_0}\left( {L - x} \right)L}}{d} + \dfrac{{k{E_0}xL}}{d} $
where $ d $ is the dielectric constant and $ L $ is the length of the dielectric introduced.
 $ \Rightarrow {C_{new}} = \dfrac{{{E_0}L}}{d}\left( {L - x\left( {1 - k} \right)} \right) $
 $ \Rightarrow {C_{new}} = \dfrac{{{E_0}L}}{d}\left( {L + x\left( {k - 1} \right)} \right) $ ………. $ (1) $
Now using this dielectric we will evaluate the potential energy which can be given by $ U $ , hence
 $ \Rightarrow U = \dfrac{1}{2}{C_{new}}{V^2} $
Substituting the value of capacitance from the equation $ (1) $ , we get
 $ \Rightarrow U = \dfrac{1}{2}\left[ {\dfrac{{{E_0}L}}{d}\left( {L + x\left( {k - 1} \right)} \right)} \right]{V^2} $ ………. $ (1) $
We know that the electrostatic pull is acting due to battery of voltage $ V $ which can be given as
 $ \Rightarrow {F_E} = - \dfrac{{dU}}{{dx}} $
Hence differentiating the equation $ (2) $ with respect to $ x $ what we get,
 $ \Rightarrow {F_E} = - \dfrac{d}{{dx}}\left( {\dfrac{1}{2}\left[ {\dfrac{{{E_0}L}}{d}\left( {L + x\left( {k - 1} \right)} \right)} \right]{V^2}} \right) $
 $ \Rightarrow {F_E} = - \dfrac{1}{2}{E_0}L\left( {k - 1} \right){V^2} $
Also given that this electrostatic force equals to gravity acting on the dielectric which results as
 $ \Rightarrow {F_E} = mg $
Hence on comparing it
 $ \Rightarrow mg = \dfrac{1}{2}{E_0}L\left( {k - 1} \right){V^2} $ ……… $ (3) $
Now the Net force $ {F_{net}} = ma $ can be given as by the difference between the initial condition $ {F_E} $ of the dielectric and its final condition $ 2{F_E} $ ,
 $ \Rightarrow {F_{net}} = 2{F_E} - {F_E} $
 $ \Rightarrow {F_{net}} = \dfrac{1}{2}{E_0}L\left( {k - 1} \right){V^2} $
Hence the acceleration can be given as
 $ \Rightarrow ma = \dfrac{1}{2}{E_0}L\left( {k - 1} \right){V^2} $
 $ \Rightarrow a = \dfrac{1}{2}\dfrac{{{E_0}L\left( {k - 1} \right){V^2}}}{m} $ ……… $ (4) $
Form equation $ (3) $ we can conclude the value of mass $ m $ as
 $ \Rightarrow mg = \dfrac{1}{2}{E_0}L\left( {k - 1} \right){V^2} $
 $ \Rightarrow m = \dfrac{1}{2}\dfrac{{{E_0}L\left( {k - 1} \right){V^2}}}{g} $
Substituting it in the equation $ (4) $ , we get
 $ \Rightarrow a = \dfrac{1}{2}\dfrac{{{E_0}L\left( {k - 1} \right){V^2}}}{{\left( {\dfrac{1}{2}\dfrac{{{E_0}L\left( {k - 1} \right){V^2}}}{g}} \right)}} $
 $ \therefore a = g $
Now the slab is half-filled with dielectric hence the height of the dielectric $ H $ will be given as
 $ \Rightarrow H = \dfrac{L}{2} = \dfrac{{0.8}}{2} = 0.4 $
Now evaluating the time by the formula for $ H $ height and $ g = 10m/{s^2} $
 $ \Rightarrow t = \sqrt {\dfrac{{2H}}{g}} $
 $ \Rightarrow t = \sqrt {\dfrac{{2 \times 0.4}}{{10}}} $
 $ \therefore t = 0.29\sec $
Hence the time the slab falls off when some mass is introduced without any impulse is $t = 0.29\sec $ .

Note:
Dielectric is a material that is insulating. In other words it is a very poor conductor of electricity. When we place dielectrics in the electric fields, then current flows through them practically as they don’t have free electrons and loose bounds.