Question

A double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is double of the other. Find the radii, if the refractive index of the material of the lens is 1.5.

Answer 1

Hint :A double convex lens is a converging lens which is thicker at the middle and thinner on the sides. Unlike mirrors, the light in the lens can pass through both sides of the lens. Hence, it has two focal lengths. In the following question we use lens maker’s formula to calculate the focal length. And after substituting the values we get the value of radii.

Complete Step By Step Answer:
The figure of a double convex lens is as follows:

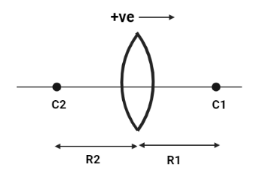
It’s given in the question that:
$f = 25cm$
$\mu = 1.5$
Let us consider ${R_1} = R$
Then,${R_2} = - 2R$
Since, ${R_2}$is on the negative side. Hence according to sign convention we will add a minus sign to the ${R_2}$
The formula to calculate the focal length of a double convex lens is:
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{R1}} - \dfrac{1}{{R2}}} \right)$
Substituting the values we get,
$ \dfrac{1}{{25}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{{ - 2R}}} \right) \\
  \dfrac{1}{{25}} = 0.5\left( {\dfrac{{2 + 1}}{{2R}}} \right) \\
  \dfrac{1}{{25}} = 0.5\left( {\dfrac{3}{{2R}}} \right) \\
  R = \dfrac{5}{{10}} \times \dfrac{{25}}{2} \times 3 \\
  R = \dfrac{{25}}{4} \times 3 \\
  R = 18.75cm \\ $
Hence,
${R_1} = 18.75$
${R_2} = 37.5$

Note :
The lens creates a real , inverted and enlarged image beyond 2F if the object is between 2F and F. It creates an imaginary, inverted and enlarged image on the same side as that of the object when the object is placed inside F. It also creates an inverted, diminished and real image between F and 2F on the opposite side of the object when the object is placed outside 2F.