
A double convex lens of focal length
Answer
504.6k+ views
Hint: There can be different types of optical lenses, based on the classification of their refracting surfaces. Lens maker formula is used to calculate the focal length of different lenses. For calculating the radius of curvature of the smaller lens, we will apply lens maker formula on the given biconvex lens.
Complete step by step answer:
A lens is a transmissive optical instrument that can focus or disperse an incident light beam using the phenomenon of refraction of light. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses or elements usually arranged along a common axis.
Lenses are classified on the basis of the curvature of the two optical surfaces. A lens is Biconvex, or double convex, if both the surfaces are convex. If both the surfaces have the same radius of curvature, the lens is called an Equiconvex lens. A lens having two concave surfaces is Biconcave, or double concave lens. If one of the surfaces of the lens is flat, the lens is called as Plano-convex or Plano-concave, depending upon the curvature of the other surface. A lens having one convex and one concave side is called a convex-concave lens.
Let us consider a thin lens with two refracting surfaces having radii of curvatures
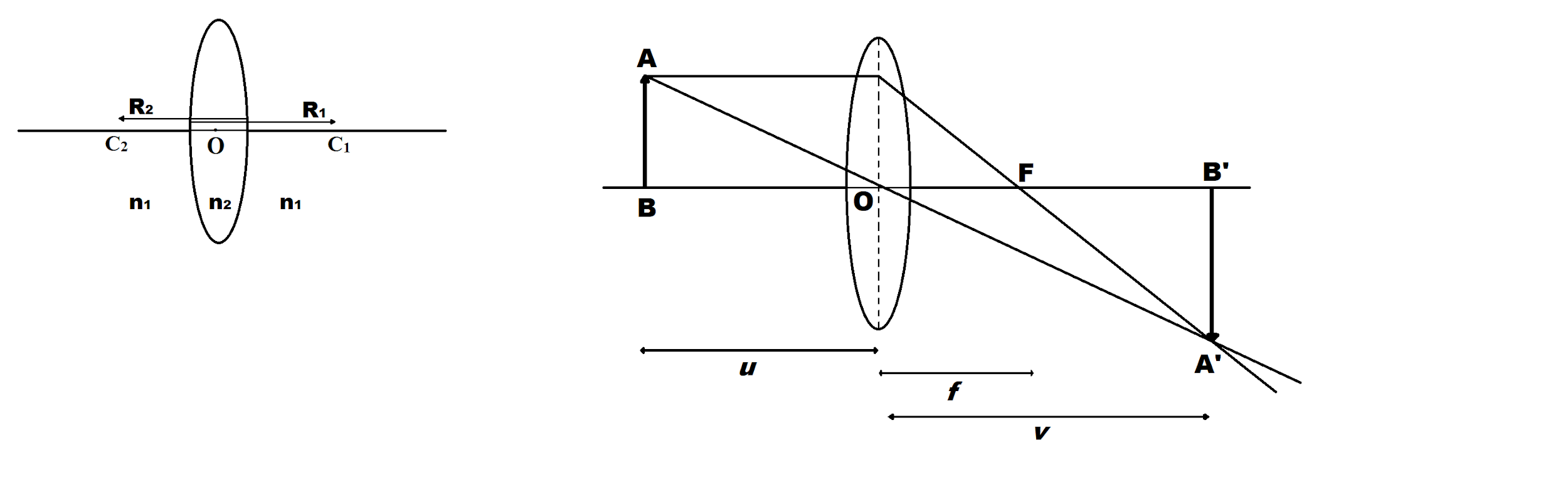
With the help of formula for refraction at a single spherical surface,
For the first surface, we have,
For the second surface, we have,
Adding the above two equations,
When
We get,
Therefore,
Where,
The above equation is known as Lens maker formula.
We are given that a double convex lens has focal length
Also,
Using lens maker formula,
Putting values,
We get,
The radius of curvature of the smaller lens is
So, the correct answer is “Option B”.
Note: While deriving the lens formula, it should be remembered that the image distance from the refraction at first surface becomes the object distance for the refraction at second surface since the light ray is passing undisturbed from the lens. Also, the refractive indices of the two spherical materials, of which lens is a part of, can also be different. In the above question, the refractive indices of both the materials were the same as the refractive index of glass.
Complete step by step answer:
A lens is a transmissive optical instrument that can focus or disperse an incident light beam using the phenomenon of refraction of light. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses or elements usually arranged along a common axis.
Lenses are classified on the basis of the curvature of the two optical surfaces. A lens is Biconvex, or double convex, if both the surfaces are convex. If both the surfaces have the same radius of curvature, the lens is called an Equiconvex lens. A lens having two concave surfaces is Biconcave, or double concave lens. If one of the surfaces of the lens is flat, the lens is called as Plano-convex or Plano-concave, depending upon the curvature of the other surface. A lens having one convex and one concave side is called a convex-concave lens.
Let us consider a thin lens with two refracting surfaces having radii of curvatures

With the help of formula for refraction at a single spherical surface,
For the first surface, we have,
For the second surface, we have,
Adding the above two equations,
When
We get,
Therefore,
Where,
The above equation is known as Lens maker formula.
We are given that a double convex lens has focal length
Also,
Using lens maker formula,
Putting values,
We get,
The radius of curvature of the smaller lens is
So, the correct answer is “Option B”.
Note: While deriving the lens formula, it should be remembered that the image distance from the refraction at first surface becomes the object distance for the refraction at second surface since the light ray is passing undisturbed from the lens. Also, the refractive indices of the two spherical materials, of which lens is a part of, can also be different. In the above question, the refractive indices of both the materials were the same as the refractive index of glass.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




