Question

(a). Draw a ray diagram to show image formation when the concave mirror produces a real, inverted and magnified image of the object.
(b). Obtain the mirror formula and then write the expression for the linear magnification.
(c). Explain two advantages of a reflecting telescope over a refracting telescope.

Answer 1

Hint: A concave mirror can form both real and virtual images. All real images are inverted while virtual images formed are erect. The mirror formula gives us a relation between the object distance, image distance and the focal length. Reflecting telescopes are those which use a mirror while lenses are used in refracting telescopes.

Complete step by step solution:
A concave mirror is a converging mirror. It has a negative focal length and it forms a real, inverted and magnified image when the object is kept between the radius of curvature and the focal length. The final image is formed beyond the radius of curvature.

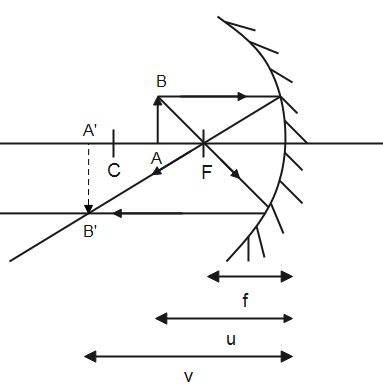
Here, $AB$ is the object and $A'B'$ is its image.
$u$ is the object distance
$v$ is the image distance
$f$ is the focal length
For a magnified image,
$f$v>R$
Therefore, the image and object are on the same side of the mirror and both the object distance and image distance are negative for a real, magnified image.
(b).

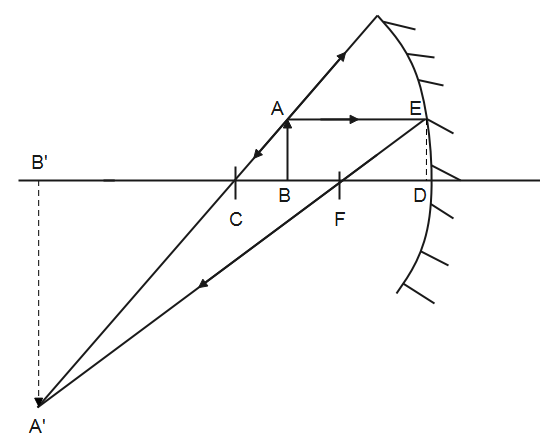
In $\Delta ABC$ and $\Delta A'B'C$
$\angle ABC=\angle A'B'C={{90}^{o}}$
$\angle ACB=\angle A'CB'$ (vertically opposite angles)
Therefore, $\Delta ABC\approx \Delta A'B'C$,
From spct,
$\dfrac{AB}{A'B'}=\dfrac{CB}{CB'}$ - (1)
Similarly, $\Delta FDE$ is similar to $\Delta FB'A'$
By spct,
$\dfrac{ED}{A'B'}=\dfrac{FD}{FB'}$ - (2)
Using eq (1) and eq (2), we get
$\dfrac{CB}{CB'}=\dfrac{FD}{FB'}$
In the above figure, we get,
$\begin{align}
  & \dfrac{CB}{CB'}=\dfrac{FD}{FB'} \\
 & \Rightarrow \dfrac{CD-BD}{B'D-CD}=\dfrac{FD}{B'D-FD} \\
 & \Rightarrow \dfrac{R-u}{v-R}=\dfrac{f}{v-f} \\
\end{align}$
In the above equation, applying cross multiplication, we get,
$\begin{align}
  & \dfrac{R-u}{v-R}=\dfrac{f}{v-f} \\
 & \Rightarrow (R-u)(v-f)=f(v-R) \\
 & \Rightarrow Rv-Rf-uv+uf=fv-Rf \\
 & \Rightarrow Rv-uv+uf=fv \\
\end{align}$
Substituting $R=2f$ in the above equation, we get,
$\begin{align}
  & 2fv-uv+uf=fv \\
 & \Rightarrow fv+uf=uv \\
\end{align}$
Dividing the equation by $uvf$,
$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$
Hence, the mirror formula is derived as $\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$.
The magnification of a mirror is the ratio of the image height to the object height. Therefore,
$m=\dfrac{A'B'}{AB}$. It is also given as-
$m=\dfrac{v}{u}$
Therefore, the mirror formula is $\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$ and the magnification is $m=\dfrac{v}{u}$.
(c). The advantages of a reflecting telescope over a refracting telescope are-
Large mirrors are easier as well as cheaper to build as well as they are easier to mount.
 Chromatic aberration is a defect in which the colours of white light spread out as the wavelengths of all colours tend to be in different focal planes. Chromatic aberration does not occur in mirrors. That is why reflecting telescopes are better than refracting telescopes.
Therefore, reflecting telescopes have many advantages over refracting telescopes.

Note: By convention, all distances measured from right to left are taken as negative and all distances measured from left to right are taken as positive. A concave mirror is known as a converging mirror and a convex mirror is known as a diverging mirror. The focal length of a concave mirror is negative while the focal length of the convex mirror is positive and the focal length of a plane mirror is infinite.