Answer
436.8k+ views
Hint: We know that electricity and magnetism are inter connected. We know that a current carrying conductor produces a magnetic field around itself. And similarly, a varying magnetic field induces a current in the coil which is kept in the near surrounding.
Formula:
$\vec F=I\vec l\times \vec B$
Complete answer:
Since electricity and magnetism are interrelated, we know that a current carrying conductor when placed in a magnetic field experiences a force. Also, the direction force is given by the right hand rule.
The force $\vec F$ experienced by a current $I$ carrying coil of length $\vec l$ which is placed in a magnetic field $\vec B$ is given as $\vec F=I\vec l\times \vec B=Ilbsin\theta$, where $\theta$ is the angle made by the length vector with respect to the magnetic field.
The direction of the force is given by the right hand rule, where the thumb, index and the middle finger are extended outwards, such that they are perpendicular to each other. Then if the thumb points towards the direction of current, the index finger points towards the direction of the magnetic field, then the middle finger points the direction of the force.
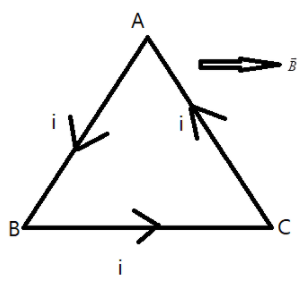
Using this we can find the force on the given triangle. Consider the line segment AB, using the right hand rule, we get, that the direction of force is outward from the paper.
Let us now consider the line segment AC, using the right hand rule, we get that the direction of force is towards the paper.
Since the length, current and the magnetic field are the same, we can say the both cancel each other.
Now consider the line segment BC, since the $\theta=0\implies sin 0=0$, thus the force due to BC is also zero.
Hence the net force due to the given triangle is also zero.
Hence the correct option is a A $0$.
Note:
We know that, Force is a vector quantity, which has both magnitude and direction.Since the force is a cross product of both the line vector and the magnetic field, we can clearly say that the force is perpendicular to both the line vector and the magnetic field.
Formula:
$\vec F=I\vec l\times \vec B$
Complete answer:
Since electricity and magnetism are interrelated, we know that a current carrying conductor when placed in a magnetic field experiences a force. Also, the direction force is given by the right hand rule.
The force $\vec F$ experienced by a current $I$ carrying coil of length $\vec l$ which is placed in a magnetic field $\vec B$ is given as $\vec F=I\vec l\times \vec B=Ilbsin\theta$, where $\theta$ is the angle made by the length vector with respect to the magnetic field.
The direction of the force is given by the right hand rule, where the thumb, index and the middle finger are extended outwards, such that they are perpendicular to each other. Then if the thumb points towards the direction of current, the index finger points towards the direction of the magnetic field, then the middle finger points the direction of the force.
Using this we can find the force on the given triangle. Consider the line segment AB, using the right hand rule, we get, that the direction of force is outward from the paper.
Let us now consider the line segment AC, using the right hand rule, we get that the direction of force is towards the paper.
Since the length, current and the magnetic field are the same, we can say the both cancel each other.
Now consider the line segment BC, since the $\theta=0\implies sin 0=0$, thus the force due to BC is also zero.
Hence the net force due to the given triangle is also zero.
Hence the correct option is a A $0$.
Note:
We know that, Force is a vector quantity, which has both magnitude and direction.Since the force is a cross product of both the line vector and the magnetic field, we can clearly say that the force is perpendicular to both the line vector and the magnetic field.
Recently Updated Pages
what is the correct chronological order of the following class 10 social science CBSE

Which of the following was not the actual cause for class 10 social science CBSE

Which of the following statements is not correct A class 10 social science CBSE

Which of the following leaders was not present in the class 10 social science CBSE

Garampani Sanctuary is located at A Diphu Assam B Gangtok class 10 social science CBSE

Which one of the following places is not covered by class 10 social science CBSE

Trending doubts
How do you graph the function fx 4x class 9 maths CBSE

Which are the Top 10 Largest Countries of the World?

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Difference Between Plant Cell and Animal Cell

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

The largest tea producing country in the world is A class 10 social science CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE