Question

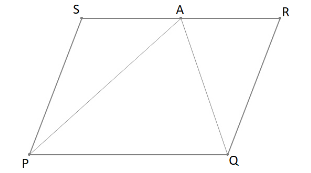
A farmer has a field in the form of a parallelogram PQRS as shown in the figure. He took the mid-point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts?
The farmer wants to sow groundnuts which are equal to the sum of pulses and paddy. How should he sow? State reasons?

Answer 1

Hint: Draw the figure after understanding the question’s need. Make a line segment from point A to midpoint of the opposite side. This will divide the field in two parallelograms and four triangles. Now try to establish a relationship between these areas.

Complete step-by-step answer:
Here in the figure, we can see that A is joined to two vertices of the parallelogram, dividing the field into three parts.
The field is divided into three triangles, i.e.$\Delta PSA$ ,$\Delta PAQ$and$\Delta QAR$.
Now for the second part of the question, we have three different crops which should be sown in three different parts of the field according to the relation given in the question.
So, we need to deduce a relation between these three areas of the triangular parts.

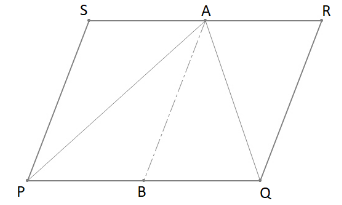
For making things more understandable, imagine a line segment $\overline {AB} $ joining midpoint of $\overline {PQ} $ and point A.
Since $\overline {AB} $ is bisecting $\overline {SR} $ and$\overline {PQ} $ , which are transversal to parallel lines $\overline {PS} $ and $\overline {RQ} $
Therefore, $AB\parallel PS$ and $AB\parallel RQ$and we get two new parallelograms PSAB and QRAB
Considering parallelogram PSAB by using the theorem that states “A diagonal of a parallelogram always divides it into two congruent triangles” and since congruent triangles always have equal areas, we can conclude that:
$\Delta PSA \cong \Delta PBA \Rightarrow Area\Delta PSA = Area\Delta PBA$ (1)
Similarly, if we use the above theorem for parallelogram QRAB, we can say that:
$\Delta QAR \cong \Delta QAB \Rightarrow Area\Delta QAR = Area\Delta QAB$ (2)
Let’s now add up these two relations (1) and (2)
$Area\Delta PSA + Area\Delta QAR = Area\Delta PBA + Area\Delta QAB$
But from our figure, we know that $\Delta PBA + \Delta QAB = \Delta PAQ$, which implies that:
$Area\Delta PSA + Area\Delta QAR = Area\Delta PAQ$
This gives us a direct relationship between the three parts of the field. And now farmers can sow paddy and pulses in the two smaller triangular parts $\Delta PSA$ & $\Delta QAR$ and groundnuts in the bigger triangular part $\Delta PAQ$.

Note: In geometry, always draw a figure using the information given in the question. Do not assume anything unless it is given in the question itself. Use the fundamental theorems associated with the geometry you are dealing with. The alternative approach to this problem can be using the theorem “A diagonal of a parallelogram divides it into two equal areas”.