
A farmer mixes two brands P and Q of cattle feed. Brand P costing Rs.250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q, costing Rs.200 per bag contain 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirement of nutrients A, B and C are 18 units, 45 units and 24 units respectively.
Determine the number of bags of each brand which should be mixed in order to produce a mixture having minimum cost per bag? What is the minimum cost of the mixture per bag?
Answer
481.5k+ views
Hint: This is a question of linear programming problem. For solving this, we will first tabulate the data. Using the given information, we will identify our objective function z and from the data, we will identify the constraints. Then we will draw graphs for the constraints (inequalities) and find their common region. From the common region, we will find the corner points. Then we will put these points one by one in the objective function z. Minimum value of z will give us minimum cost and the point (value of x,y) where cost is minimum.
Complete step by step answer:
Let us first suppose that the mixture contains x bags of brand P and y bags of brand Q.
Brand P contains 3 units of element A, 2.5 units of element B and 2 units of element C.
Brand Q contains 1.5 units of element A, 11.25 units of element B and 3 units of element C.
Minimum requirement of element A is 18 units, element B is 45 units and element C is 24 units. Tabulating this data we have,
Now let us form the constraints using the table,
For element A we have,
Dividing both sides by 1.5 we have
Simplifying we get
For element B, we have
Dividing by 1.25 we get
Simplifying we get
For element C we have
Also we know that the number of bags cannot be negative so
Now we need to minimize the cost. Let us suppose objective function is z which we need to minimize.
Cost of brand P is Rs.250 and cost of brand Q is Rs.200.
Hence we need to minimize the function.
Now objective function z is subject to the constraints given by (1), (2), (3), (4). So our LPP looks like this,
Minimize
Now let us draw a graph for all the constraints and find the common point.
Coordinates for inequalities can be formed as,
For
For
For
Our graph looks like this,
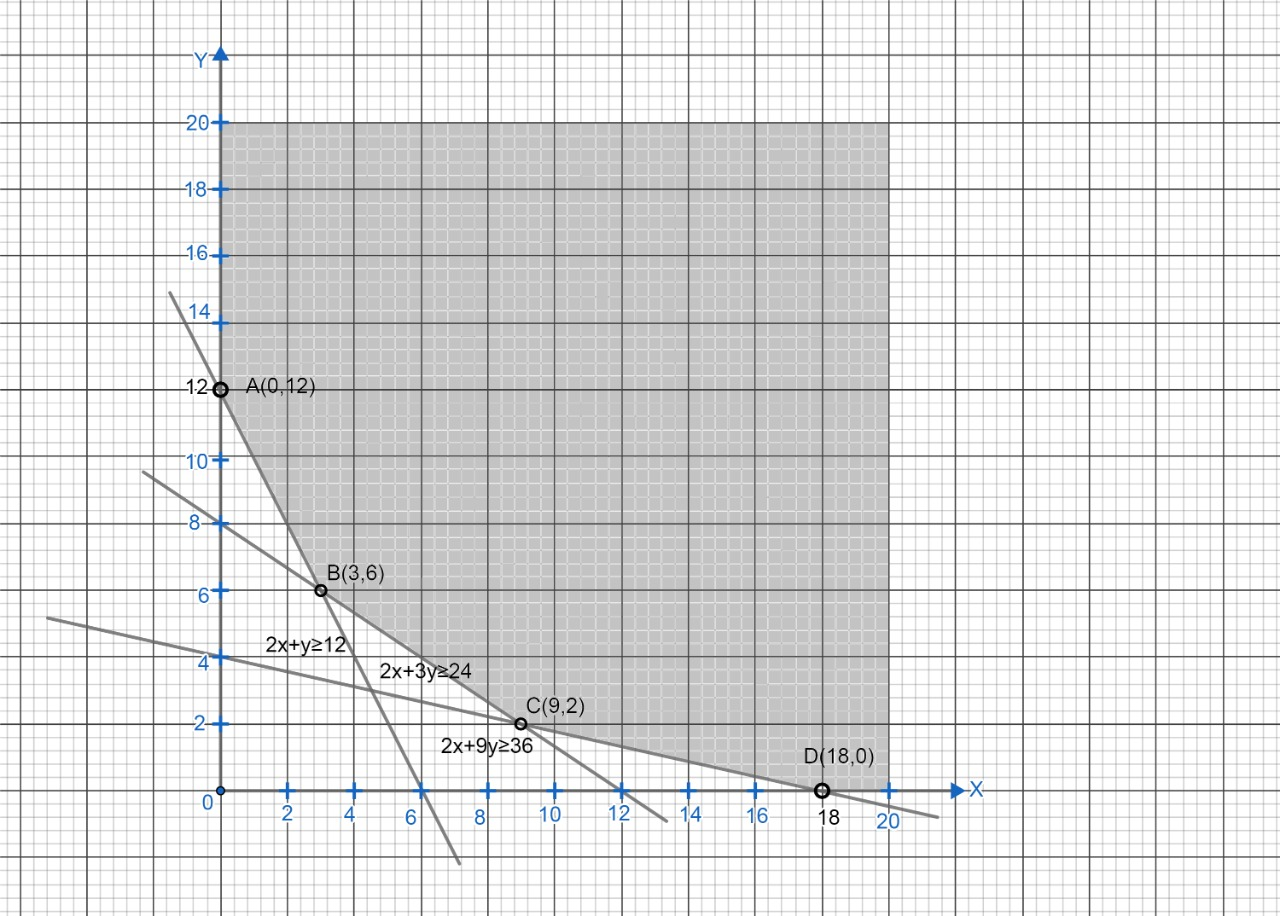
From the graph we can see that the corner points are A(0,12), B(3,6), C(9,2) and D(18,0).
Let us use this value in z, and find minimum value of z
For A(0,12)
For B(3,6)
For C(9,2)
For D(18,0)
As we can see, we have minimum z at B(3,6).
Therefore, the minimum cost is Rs.1950.
Required values of x and y are 3, 6 respectively.
Hence, the cost will be minimum if the mixture contains 3 bags of brand P and 6 bags of brand Q.
Also the minimum cost will be Rs.1950.
Note: Students should note that the region is unbounded. Maximum value of such LPP cannot be found. To check if the obtained value is minimum they can draw the inequality 250x+200y<1950 on graph and check for any common point between feasible region and the inequality. If there does not exist any point the answer is correct.
Complete step by step answer:
Let us first suppose that the mixture contains x bags of brand P and y bags of brand Q.
Brand P contains 3 units of element A, 2.5 units of element B and 2 units of element C.
Brand Q contains 1.5 units of element A, 11.25 units of element B and 3 units of element C.
Minimum requirement of element A is 18 units, element B is 45 units and element C is 24 units. Tabulating this data we have,
| Brand | Number of boys | Element A | Element B | Element C |
| P | x | 3 units | 2.5 units | 2 units |
| Q | y | 1.5 units | 11.25 units | 3 units |
| Least requirement | 18 units | 45 units | 24 units |
Now let us form the constraints using the table,
For element A we have,
Dividing both sides by 1.5 we have
Simplifying we get
For element B, we have
Dividing by 1.25 we get
Simplifying we get
For element C we have
Also we know that the number of bags cannot be negative so
Now we need to minimize the cost. Let us suppose objective function is z which we need to minimize.
Cost of brand P is Rs.250 and cost of brand Q is Rs.200.
Hence we need to minimize the function.
Now objective function z is subject to the constraints given by (1), (2), (3), (4). So our LPP looks like this,
Minimize
Now let us draw a graph for all the constraints and find the common point.
Coordinates for inequalities can be formed as,
For
| x | 6 | 0 |
| y | 0 | 12 |
For
| x | 0 | 18 |
| y | 4 | 0 |
For
| x | 0 | 12 |
| y | 8 | 0 |
Our graph looks like this,

From the graph we can see that the corner points are A(0,12), B(3,6), C(9,2) and D(18,0).
Let us use this value in z, and find minimum value of z
For A(0,12)
For B(3,6)
For C(9,2)
For D(18,0)
As we can see, we have minimum z at B(3,6).
Therefore, the minimum cost is Rs.1950.
Required values of x and y are 3, 6 respectively.
Hence, the cost will be minimum if the mixture contains 3 bags of brand P and 6 bags of brand Q.
Also the minimum cost will be Rs.1950.
Note: Students should note that the region is unbounded. Maximum value of such LPP cannot be found. To check if the obtained value is minimum they can draw the inequality 250x+200y<1950 on graph and check for any common point between feasible region and the inequality. If there does not exist any point the answer is correct.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




