Question

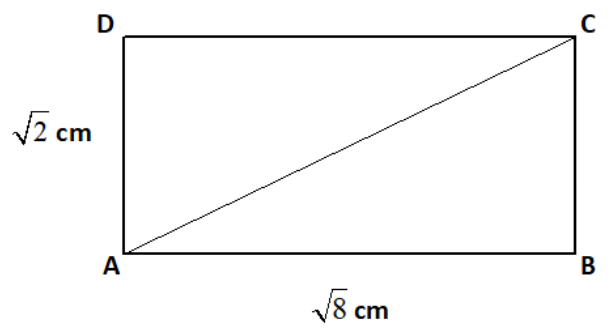
(a) Find the area and perimeter of the rectangle in figure.
(b) What is the length of AC?

Answer 1

Hint: We are given the length and the breadth of the rectangle and we need to find the area and the perimeter of the given rectangle. Also, we need to find the length of AC, which is called the diagonal of the rectangle. For that we see that vertices A, B and C form a right angled triangle right angled at B(angles of the rectangle are \[{90^ \circ }\]). Therefore, we can use Pythagoras Theorem in triangle ABC and then find the length of AC, which is the hypotenuse as base and height are given as the sides of the rectangle.
Formula Used:
Perimeter of the rectangle\[ = 2(length + breadth)\]
Area of the rectangle\[ = length \times breadth\]
Pythagoras theorem: \[{(Hypotenuse)^2} = {(Base)^2} + {(Perpendicular)^2}\]

Complete step-by-step solution:
We are given, The length and breadth of the rectangle.
Length = AB=\[\sqrt 8 \]cm
Breadth=AD=\[\sqrt 2 \]cm
Also, we know that opposite sides of a rectangle are equal.
\[\therefore \]AB = CD = \[\sqrt 8 \]cm and BC = AD = \[\sqrt 2 \]cm
a). Now, find the area of the rectangle.
We know,
Area of the rectangle \[ = Length \times Breadth\]
\[ = (\sqrt 8 \times \sqrt 2 )\]cm2
\[ = \sqrt {16} \]${cm}^2$
\[ = \sqrt {{4^2}} \]${cm}^2$
\[ = 4\]cm2 (\[\sqrt {{x^2}} = \pm x\] , but area can never be negative)
\[\therefore \]The area of the rectangle \[ = 4\]${cm}^2$
Now, find the perimeter of the rectangle.
We know,
Perimeter of the rectangle\[ = 2(length + breadth)\]
\[ = 2(\sqrt 8 + \sqrt 2 )\]cm
\[ = 2(\sqrt {{2^3}} + \sqrt 2 )\] cm
\[ = 2(\sqrt {{2^2} \times 2} + \sqrt 2 )\] cm
\[ = 2(\sqrt {{2^2}} \times \sqrt 2 + \sqrt 2 )\]cm
\[ = 2(2 \times \sqrt 2 + \sqrt 2 )\]cm
\[ = 2(3\sqrt 2 )\]cm
\[ = 6\sqrt 2 \]cm
\[\therefore \]The perimeter of the rectangle\[ = 6\sqrt 2 \]cm
b). We need to find the length of AC.
We see that Triangle ABC is a right angled triangle and so we can apply Pythagoras Theorem in Triangle ABC.
We see, AB is the base and BC is the perpendicular of Triangle ABC.
Also, AB = \[\sqrt 8 \]cm and BC = \[\sqrt 2 \]cm
So, using Pythagoras Theorem on Triangle ABC, we have
\[{(Hypotenuse)^2} = {(Base)^2} + {(Height)^2}\]
\[\Rightarrow {(AC)^2} = {(AB)^2} + {(BC)^2}\]
\[\Rightarrow {(AC)^2} = {(\sqrt 8 )^2} + {(\sqrt 2 )^2}\]
\[\Rightarrow {(AC)^2} = 8 + 2\]
\[\Rightarrow {(AC)^2} = 10\]
\[\Rightarrow AC = \sqrt {10} \] (Square rooting both the sides)
\[\therefore \] Length of AC\[ = \sqrt {10} \]cm

Note: We need to keep in mind that Pythagoras Theorem can be applied on the Right angled triangle only. Also, we need to make sure that while square rooting both plus and minus sign comes but as Sides, area, perimeter can never be negative, we ignore the negative sign and consider only positive signs. And, most importantly, we forget to add units for sides, area and perimeter. So, we need to be careful with that.