Question

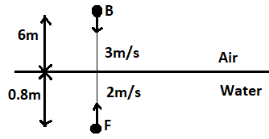
A fish, $F$in the pond, is at a depth of $0.8m$ from water surface and is moving vertically upwards with velocity $2m{s^{ - 1}}$ . At the same instant, a bird $B$is at a height of $6m$from water surface and is moving downwards with velocity $3m{s^{ - 1}}$. At this instant both are on the same vertical lines as shown in the figure. Which of the following statement(s) is(are) correct?
(A) Height of $B$, observed by $F$(from itself) is equal to $8.00m$.
(B) Depth of $F$, observed by $B$ (from itself) is equal to $6.60m$.
(C) Velocity of $B$, observed by $F$(relative from itself) is equal to $5.00m{s^{ - 1}}$.
(D) Velocity of $F$, observed by $B$ (relative from itself) is equal to $4.50m{s^{ - 1}}$.

$\mu = \dfrac{4}{3}$

Answer 1

Hint:The actual height and depth at which the objects view each other are the sum of the apparent and real parameters. Thus, we need to find the apparent quantities and then add them to the real quantities.

Formulas used:
The formula $\dfrac{{d'}}{{\mu '}} = \dfrac{d}{\mu }$ where $d'$ is the apparent depth of $F$, $d$ is the real depth of $F$, $\mu '$is the refractive index of air and $\mu $ is the refractive index of water.The formula $\dfrac{{h'}}{\mu } = \dfrac{h}{{\mu '}}$ where $h'$ is the apparent height of $B$ , $h$ is the real height of $B$ , $\mu '$is the refractive index of air and $\mu $ is the refractive index of water.

Complete step by step answer:
It is given in the figure that the refractive index of water $\mu $ is equal to $\dfrac{4}{3}$ and the refractive index of air $\mu '$ is always assumed to be $1$ .
First let’s check the option A.
From the figure, it is clear that the real height $h$ is equal to $6m$and real depth $d$ is equal to $0.8m$.
Using the formula $\dfrac{{h'}}{\mu } = \dfrac{h}{{\mu '}}$,
after substituting the values we get
$ \Rightarrow h' = \dfrac{\mu }{{\mu '}} \times h = \dfrac{4}{3} \times \dfrac{6}{1} = 8m$
$\therefore $ Height of $B$, observed by $F$(from itself) is equal to $h' + d = 8 + 0.8 = 8.8m$
Thus, the option A is not correct.
For option B,
From the figure, it is clear that the real depth $d$ is equal to $0.8m$ and the real height $h$ is equal to $6m$.
Using the formula $\dfrac{{d'}}{{\mu '}} = \dfrac{d}{\mu }$ ,
after substituting the values we get
$ \Rightarrow d' = \dfrac{{0.8}}{{\dfrac{4}{3}}} \times 1 = 0.6m$
$\therefore $ The depth of $F$, observed by $B$ (from itself) is equal to $d' + h = 0.6 + 6 = 6.6m$.
Thus, the option B is correct.
For option C,
It is given in the figure that the velocity of the fish ${v_F}$ is equal to $2m{s^{ - 1}}$ and the velocity of the bird ${v_B}$ is $3m{s^{ - 1}}$.
$\therefore $ The velocity of $B$, observed by $F$(relative from itself) is equal to ${v_F} + \dfrac{1}{\mu }{v_B} = 2 + (\dfrac{1}{1} \times 3) = 5m{s^{ - 1}}$
Thus, option C is correct.
For option D,
It is given in the figure that the velocity of the fish ${v_F}$ is equal to $2m{s^{ - 1}}$ and the velocity of the bird ${v_B}$ is $3m{s^{ - 1}}$.
$\therefore $ The velocity of $F$, observed by $B$ (relative from itself) is equal to $\dfrac{1}{{\mu '}}{v_F} + {v_B} = (\dfrac{1}{{\dfrac{4}{3}}} \times 2) + 3 = 4.5m{s^{ - 1}}$
Thus, option D is correct.

Hence,the correct options are B, C and D.

Note:It could be confusing about what refractive index is to be considered for a specific parameter like height or depth. So it should be remembered that length$ \propto $refractive index that is the refractive index of that medium is to be considered from which the image is being viewed.