Question

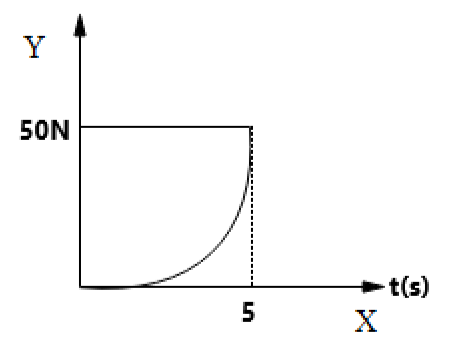
A force F is applied to the initially stationary cart. The variation of force with time is shown in the figure. The speed of cart at $t=5s$ is?
A. $10m{{s}^{-1}}$
B. $8.33m{{s}^{-1}}$
C. $2m{{s}^{-1}}$
D. Zero

Answer 1

Hint:We are given the force-time graph of a body going under non-uniformly accelerated motion. For a body going under non-uniformly accelerated motion, the Newton’s equations of motion cannot be used. A non-uniformly accelerated motion is one where the body accelerates or decelerates at any instances of time during the observed motion. Thus, in this case we take the instantaneous velocity of the body under consideration.

Complete step-by-step solution:
The slope on the position-time graph is equal to the instantaneous velocity. This is a way of finding instantaneous velocity without using calculus.
The equation of the given parabolic graph is:
$\begin{align}
  & F\propto {{t}^{2}} \\
 & \Rightarrow F=k{{t}^{2}} \\
\end{align}$
Where,
$F=$ force (on y-axis)
$t=$time (on x-axis)
$k=$proportionality constant
$\begin{align}
  & \Rightarrow 50=k{{\left( 5 \right)}^{2}} \\
 & \Rightarrow k=2 \\
\end{align}$
$\therefore F=2{{t}^{2}}$

We also know that, $F=ma$
Where,
$m=$mass of body $=10Kg$(here)
$a=$acceleration of body
$\begin{align}
  & \Rightarrow ma=2{{t}^{2}} \\
 & \Rightarrow \left( 10 \right)a=2{{t}^{2}} \\
\end{align}$
$\Rightarrow a=0.2{{t}^{2}}$ …………….. equation (1)

To find the instantaneous velocity \[\left( {{V}_{\text{instantaneous}}} \right)\], we have to divide an infinitesimally-small displacement with an infinitesimally-small time interval which would practically be equal to an indeterminate form of limit (or $\dfrac{0}{0}$). Hence, sir Isaac Newton invented a whole new form of mathematics called calculus.
$\begin{align}
  & {{V}_{\text{instantaneous}}}=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{x\left( t+h \right)-x\left( t \right)}{h} \\
 & \text{Or }{{V}_{\text{instantaneous}}}=\dfrac{dx}{dt} \\
\end{align}$

Similarly, instantaneous acceleration, ${{a}_{\text{instantaneous}}}=\dfrac{dv}{dt}$
$\begin{align}
  & \Rightarrow \int{dv}=\int{{{a}_{\text{instantaneous}}}.dt} \\
 & \Rightarrow v=\int{{{a}_{\text{instantaneous}}}.dt} \\
\end{align}$

From equation (1),
$\Rightarrow v=\int\limits_{0}^{t}{0.2{{t}^{2}}.dt}$
At $t=5s,$
$\Rightarrow v=\int\limits_{0}^{5}{0.2{{t}^{2}}.dt}$
$\Rightarrow v=0.2\left[ \dfrac{{{t}^{3}}}{3} \right]_{0}^{5}$
$\begin{align}
  & \Rightarrow v=0.2\left( \dfrac{{{5}^{3}}-{{0}^{3}}}{3} \right) \\
 & \Rightarrow v=0.2\left( \dfrac{125}{3} \right) \\
 & \Rightarrow v=8.33m{{s}^{-1}} \\
\end{align}$
The speed of the cart at $t=5s$ is $8.33m{{s}^{-1}}$.

Therefore, the correct option is (B) $8.33m{{s}^{-1}}$.

Note:
The instantaneous velocity is the velocity of an object at a particular moment in time. This is different from the average velocity of the object. The average velocity is equal to the total displacement divided by the total time taken during the motion. It does not change with the acceleration or deceleration of the object taking place during the motion.