Question

A galvanometer of resistance $25ohm$ is connected to a battery of $2V$ along with a resistance in series. When the value of this resistance is $3000$, a full scale deflection of 30 units is obtained in the galvanometer. In order to reduce this deflection to 20 units. The resistance in series will be

Answer 1

Hint When calculating the current passing through the galvanometer, we have to consider the resistance of the galvanometer as well as the resistor connected in series. The higher the resistance in series, the lower the current through the galvanometer.

Formula Used:
We have used only Ohm’s law in this problem. It is given by
$V = IR$
Where $V$ is the voltage applied.
$I$ is the current through the resistor.
$R$ is resistance.

Complete step by step answer:
We can visualize the circuit given in this problem as follows

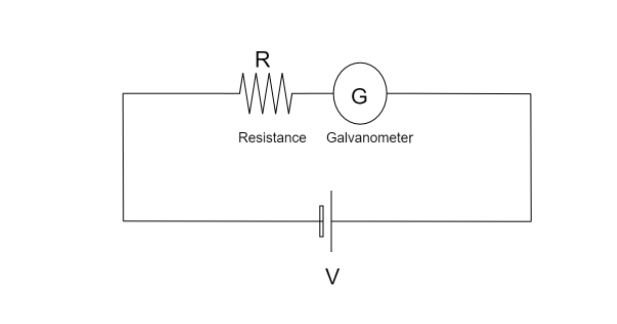
According to Ohm’s law, we know that
$V = IR$
This formula can be modified for this problem as
$V = {I_g}\left( {R + G} \right)$
$ \Rightarrow {I_g} = \dfrac{V}{{\left( {R + G} \right)}}$ $ - - - - (1)$
Where $G$ is the resistance offered by the galvanometer which is given as $G = 25\Omega $.
We have connected a battery of potential $V = 2V$ to the galvanometer and resistor of resistance, $R = 3000\Omega $.
${I_g} = \dfrac{2}{{\left( {3000 + 25} \right)}}$ $ - - - - (2)$
We know that Galvanometers are used to detect current and it is given that a full-scale deflection of 30 units is observed.
So, we can write that
${I_g} = 30 \times g$ $ - - - - (3)$
$ \Rightarrow g = \dfrac{{{I_g}}}{{30}}$ $ - - - - (4)$
Where $g$ is the figure of merit of the galvanometer.
Using equation $(2)$ and $(4)$, we get the value of the figure of merit as
$g = \dfrac{2}{{\left( {3000 + 25} \right) \times 30}}$ $ - - - - (5)$
Initially, for $R = 3000\Omega $ deflection was 30 units in the galvanometer.
Now, we need a deflection of $20$ units in the galvanometer.
Similarly, it can be written that the required current is
${I_g} = 20 \times g$ $ - - - - (6)$
Using the equation$(1)$, we know that current is given by the formula
${I_g} = \dfrac{V}{{\left( {R' + G} \right)}}$ $ - - - - (7)$
Where $R'$is the adjusted resistance.
So comparing equations $(6)$ and $(7)$,
$20 \times g = \dfrac{V}{{\left( {R' + G} \right)}}$
$\left( {R' + G} \right) = \dfrac{V}{{20 \times g}}$
Putting $V = 2V$and the figure of merit $(g)$ from the equation$(5)$, we get
$\left( {R' + G} \right) = \dfrac{2}{{20}} \times \dfrac{{\left( {3000 + 25} \right) \times 30}}{2}$
$ \Rightarrow \left( {R' + G} \right) = 4537.5$
Using $G = 25\Omega $
$R' = 4512.5\Omega $

Thus, the resistance that we need to get a deflection of $20$ units in the galvanometer is $4512.5\Omega $.

Note Be very careful with the position of the external resistor. If the resistor is in series we follow this method. If the resistance is in parallel, then you have to derive the appropriate formula for such circuits. If the resistance is in parallel, the higher the resistance value, the more current will pass through the galvanometer.