Question

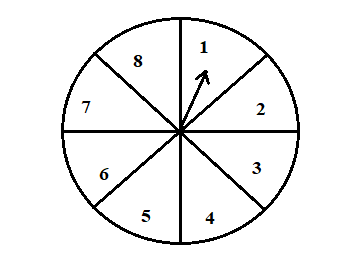
A game of chances of spinning an arrow which comes to rest pointing at one of the numbers $1,2,3,4,5,6,7,8$ (see figure below), and these are equally likely outcomes. What is the probability that it will be at a point at

A. 8
B. An odd number
C. A number greater than 2
D. A number less than 9

Answer 1

Hint: First of all, observe the given spinning wheel and write down the possible outcomes of which the arrow stops when it comes to rest. Then find the number of favourable outcomes for each event to get the required probability.

Complete step-by-step answer:
Here the possible outcomes are $1,2,3,4,5,6,7,8$
So, the total number of possible outcomes = 8
A. 8
We have to find the probability of that the arrow stops at 8
Here the favourable outcomes are 8
The number of favourable outcomes = 1
The total number of possible outcomes = 8
We know that the probability of an event \[E\] is given by \[P\left( E \right) = \dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{Total number of outcomes}}}}\]
Hence, $P\left( 8 \right) = \dfrac{1}{8}$
Thus, the required probability is $\dfrac{1}{8}$.

B. An odd number
We have to find the probability that the arrow stops at an odd number
Here the favourable outcomes are 1,3,5,7
So, the number of favourable outcomes = 4
The total number of possible outcomes = 8
We know that the probability of an event \[E\] is given by \[P\left( E \right) = \dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{Total number of outcomes}}}}\]
Hence, $P\left( {{\text{an odd number}}} \right) = \dfrac{4}{8} = \dfrac{1}{2}$
Thus, the required probability is $\dfrac{1}{2}$.

C. A number greater than 2
We have to find the probability that the arrow stops at a number greater than 2
Here the favourable outcomes are 3,4,5,6,7,8
So, the number of favourable outcomes = 6
The total number of possible outcomes = 8
We know that the probability of an event \[E\] is given by \[P\left( E \right) = \dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{Total number of outcomes}}}}\]
Hence, $P\left( {{\text{a number greater than 2}}} \right) = \dfrac{6}{8} = \dfrac{3}{4}$
Thus, the required probability is $\dfrac{3}{4}$.

D. A number less than 9
We have to find the probability that the arrow stops at a number less than 9
Here the favourable outcomes are 1,2,3,4,5,6,7,8
So, the number of favourable outcomes = 8
The total number of possible outcomes = 8
We know that the probability of an event \[E\] is given by \[P\left( E \right) = \dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{Total number of outcomes}}}}\]
Hence, $P\left( {{\text{a number less than 9}}} \right) = \dfrac{8}{8} = 1$
Thus, the required probability is 1.

Note: The probability of an event \[E\] is given by \[P\left( E \right) = \dfrac{{{\text{Number of favourable outcomes}}}}{{{\text{Total number of outcomes}}}}\]. The probability of an event is always lying between 0 and 1 i.e., \[0 \leqslant P\left( E \right) \leqslant 1\].