
A geostationary satellite is orbiting around an arbitrary planet ‘P’ at a height of
(A)
(B)
(C)
(D)
Answer
138.9k+ views
Hint: In order to solve this question, we will use Kepler's third law to find the relation between the time period for a geostationary satellite and the time period for given another satellite, and then, we will solve both equations to find the time period of another given satellite.
Formula used:
If T is the time period and R is the semi-major axis of an object circulating around any other celestial body such as a satellite revolving around planets is given by
Complete answer:
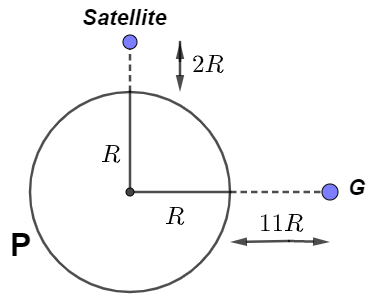
From the drawn diagram, we can see that G is the geostationary satellite orbiting around a planet P at a height of
And let ‘T’ be the time period of a geostationary satellite which is
Now, for the given another satellite which is at a height of
Divide equations (i) and (ii) by equating each other by removing the proportionality constant we get,
So, the Time period of the given satellite is
Hence, the correct option is (B)
Note: It should be remembered that the other two laws of Kepler are such that planets revolve around the sun in an elliptical orbit having the sun as one of the foci and all planets cover the equal area in equal intervals of time while revolving around the sun.
Formula used:
If T is the time period and R is the semi-major axis of an object circulating around any other celestial body such as a satellite revolving around planets is given by
Complete answer:

From the drawn diagram, we can see that G is the geostationary satellite orbiting around a planet P at a height of
And let ‘T’ be the time period of a geostationary satellite which is
Now, for the given another satellite which is at a height of
Divide equations (i) and (ii) by equating each other by removing the proportionality constant we get,
So, the Time period of the given satellite is
Hence, the correct option is (B)
Note: It should be remembered that the other two laws of Kepler are such that planets revolve around the sun in an elliptical orbit having the sun as one of the foci and all planets cover the equal area in equal intervals of time while revolving around the sun.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
EMI starts from ₹2,625 per month
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




