Question

A glass prism has refractive index $\sqrt 2 $ and refracting angle ${30^o}$. One of the refracting surfaces of the prism is silvered. A beam of monochromatic light will retrace its path if its angle of incidence on the unsilvered refracting surface of the prism is
$
  (a){\text{ 0}} \\
  (b){\text{ }}\dfrac{\pi }{6} \\
  (c){\text{ }}\dfrac{\pi }{4} \\
  (d){\text{ }}\dfrac{\pi }{3} \\
 $

Answer 1

Hint: In this question consider an incident ray is shown when incident on the silvered is coated side of the prism such that the incident angle be $i$. Trace the path and use the fact that the refracted ray must strike at 90 degree on the other surface of the prism. Apply the angle sum property in triangle ABC, to find angle $\angle BCA$ (see the figure). As PQ is a normal to the prism thus angle R can easily be found. Apply the Snell’s law at point C. This will help get the right answer.

Complete step-by-step solution:

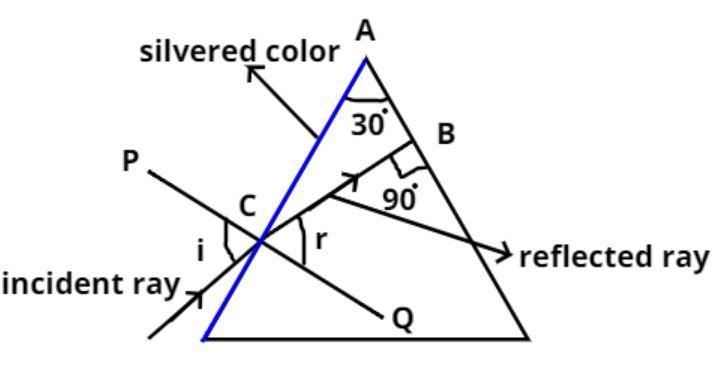
The pictorial representation of the given problem is shown above.
One of the reflecting surfaces is silvered as shown in the figure by blue color.
The refractive index $\left( \mu \right)$ of the prism is $\sqrt 2 $ and refracting angle $\angle CAB = {30^o}$ as shown in the figure.
Now it is given that a beam of monochromatic light will trace its path if the angle of incidence is?
Now an incident ray is shown when is incident on the silvered coated side of the prism, the angle of incidence is $i$, now to trace its path the refracted ray must strike at 90 degree on the other surface of the prism as shown in the figure.
Let PQ be the normal on the surface of the prism.
And (r) be the refracting angle of the monochromatic light.
Now in triangle ABC, the sum of all angles is 180 degrees.
$ \Rightarrow \angle CAB + \angle BCA + \angle CBA = {180^o}$
Let, $\angle BCA$ = x
$ \Rightarrow {30^o} + x + {90^o} = {180^o}$
Now simplify this we have,
$ \Rightarrow x = {180^o} - {120^0} = {60^o}$
Now PQ is a normal to the prism, so $\angle ACQ = {90^o}$
$ \Rightarrow \angle ACQ = \angle ACB + \angle BCQ = {90^o}$
$ \Rightarrow x + r = {90^o}$
Now substitute the value we have,
$ \Rightarrow r = {90^o} - {60^o} = {30^o}$
Now according to Snell’s law we have,
$ \Rightarrow {\mu _1}\sin i = \mu \sin r$
Where, ${\mu _1}$ is the refractive index of the air which is always 1.
Now substitute all the values in the above equation we have,
$ \Rightarrow \left( 1 \right)\sin i = \left( {\sqrt 2 } \right)\sin {30^o}$
$ \Rightarrow \sin i = \left( {\sqrt 2 } \right)\dfrac{1}{2}$, $\left[ {\because \sin {{30}^o} = \dfrac{1}{2}} \right]$
$ \Rightarrow \sin i = \dfrac{1}{{\sqrt 2 }}$, $\left[ {\because \dfrac{{\sqrt 2 }}{2} = \dfrac{1}{{\sqrt 2 }}} \right]$
$ \Rightarrow \sin i = \sin {45^o}$, $\left[ {\because \sin {{45}^o} = \dfrac{1}{{\sqrt 2 }}} \right]$
Now on comparing we have,
$ \Rightarrow i = {45^o} = \dfrac{\pi }{4}$
So the angle of incidence is $\dfrac{\pi }{4}$.
So this is the required answer.
Hence option (C) is the correct answer.

Note – It is important to understand the concept of angle of prism as any angle inside a prism can’t be considered as the angle of the prism. So angle of prism is specifically defined as the angle between those two surfaces of the prism one from which the light enters the prism and the one from which the light goes out of the prism after the refraction. In this case it was the angle between the silvered and the unsilvered surface of the prism.