Question

A glass prism of refracting angle ${{60}^{\circ }}$ and refractive index 1.5, is completely immersed in water of refractive index 1.33. Calculate the angle of minimum deviation of the prism in this situation. (Given, ${{\sin }^{-1}}0.56={{34.3}^{\circ }}$)

Answer 1

Hint: When we pass light through a parallel-side glass slab, the refracted ray emerges from the other side without any deviation, parallel to the incident ray. If we pass the same ray through a prism where the two sides are not parallel to each other, then the ray of light does get deviated compared to the incident ray. Therefore, any ray of light passing through a prism will undergo some deviation in its angle during refraction and that deviation will have a minimum value at a certain angle of incidence of light ray.

Complete step-by-step solution:
We know that refractive index of water, ${{\mu }_{water}}=1.33$
And given that refractive index of glass prism (with respect to air), ${{\mu }_{lens}}=1.5$
But refractive index changes with respect to the surrounding of the refracting surface.

Thus, refractive index of glass prism with respect to water, ${}^{water}{{\mu }_{lens}}=\dfrac{{{\mu }_{lens}}}{{{\mu }_{water}}}$
\[\begin{align}
  & \Rightarrow {}^{water}{{\mu }_{lens}}=\dfrac{1.5}{1.33} \\
 & \Rightarrow {}^{water}{{\mu }_{lens}}=\dfrac{9}{8} \\
\end{align}\]
The refractive index of prism is also expressed as:
\[{}^{water}{{\mu }_{lens}}=\dfrac{\sin \left[ \dfrac{A+{{\delta }_{m}}}{2} \right]}{\sin \left[ \dfrac{A}{2} \right]}\]
Where,
$A=$ angle of prism
${{\delta }_{m}}=$ angle of minimum deviation of prism

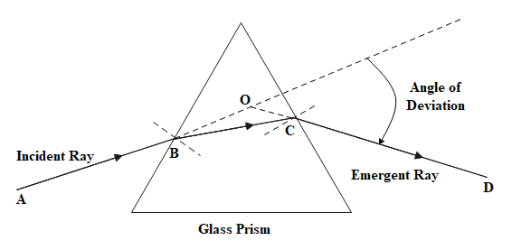
Here, $A={{60}^{\circ }},{}^{water}{{\mu }_{lens}}=\dfrac{9}{8}$
$\begin{align}
  & \Rightarrow \dfrac{9}{8}=\dfrac{\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right]}{\sin \left[ \dfrac{{{60}^{\circ }}}{2} \right]} \\
 & \Rightarrow \dfrac{9}{8}=\dfrac{\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right]}{\sin {{30}^{\circ }}} \\
\end{align}$

Since, $\sin {{30}^{\circ }}=\dfrac{1}{2},$$\Rightarrow \dfrac{9}{8}=\dfrac{\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right]}{\dfrac{1}{2}}$
 $\begin{align}
  & \Rightarrow \dfrac{9}{8}.\dfrac{1}{2}=\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right] \\
 & \Rightarrow \dfrac{9}{16}=\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right] \\
 & \Rightarrow 0.56=\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right] \\
\end{align}$

Given, ${{\sin }^{-1}}0.56={{34.3}^{\circ }}$,$\Rightarrow \sin {{34.3}^{\circ }}=0.56$
 $\begin{align}
  & \Rightarrow \sin {{34.3}^{\circ }}=\sin \left[ \dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \right] \\
 & \Rightarrow {{34.3}^{\circ }}=\dfrac{{{60}^{\circ }}+{{\delta }_{m}}}{2} \\
 & \Rightarrow {{34.3}^{\circ }}\times 2={{60}^{\circ }}+{{\delta }_{m}} \\
 & \Rightarrow {{\delta }_{m}}={{68.6}^{\circ }}-{{60}^{\circ }} \\
\end{align}$
$\therefore {{\delta }_{m}}={{8.6}^{\circ }}$

Therefore, the angle of minimum deviation is ${{8.6}^{\circ }}$.

Note:
For a given prism, the angle of deviation only depends on the angle of incidence. Studying from the angle of incidence equal to ${{0}^{\circ }}$, as we increase the angle of incidence, the angle of deviation slowly decreases to a minimum value and then shoots up to infinity as we keep increasing the angle of incidence of the light ray. This can be observed easily with the graph of angle of incidence ($i$) v/s angle of deviation ($\delta $).