Question

A golf ball has a diameter equal to $4.1cm$. Its surface has $150$ dimplets each of radius $2mm$. Calculate total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.

Answer 1

Hint: In this question we will use some important formulae for finding the surface area of the spherical golf ball. Here, we have given some parameters we will use them to find out the total surface area of that golf ball by using the formula:
Surface area of a sphere = $4\pi {r^2}$. And then we will remove the area of each dimplet from the total surface area.

Complete step-by-step answer:
Given that, diameter of golf ball = $4.1cm$
$ \Rightarrow {\text{ radius of the ball = }}\dfrac{{diameter}}{2} = \dfrac{{4.1}}{2}cm$
Radius of each dimplet = $2mm = \dfrac{2}{{10}}cm$.
We have,
$ \Rightarrow $ Surface area of the golf ball = $4\pi {r^2}$
$ \Rightarrow $ Surface area of the golf ball = $4 \times \pi \times {\left( {\dfrac{{4.1}}{2}} \right)^2} = 16.81\pi c{m^2}$ .
Here, there are a total of 150 dimplets present on the surface of the golf ball. Each dimplet occupies some area.
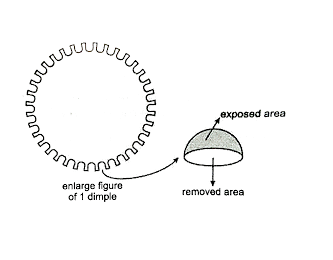
In case of each dimple, surface area is equals to $\pi {r^2}$ ( where r is the radius of each dimple ) is removed from the total surface area of the golf ball where as the surface area of the hemisphere i.e. $2\pi {r^2}$ is exposed from the surroundings.

So, total surface area exposed to the surroundings =
Surface area of the ball - $150 \times \pi {r^2} + 150 \times 2\pi {r^2}$ .
$
   = 16.81\pi + 150\pi {r^2} \\
   = \left\{ {16.81\pi + 150 \times \pi \times {{\left( {\dfrac{2}{{10}}} \right)}^2}} \right\}c{m^2} \\
   = (16.81\pi + 6\pi )c{m^2} \\
   = 22.81\pi c{m^2} \\
$
Here we will take $\pi = \dfrac{{22}}{7}$.
Therefore, total surface area exposed to the surrounding = $\left( {22.81 \times \dfrac{{22}}{7}} \right)c{m^2} = 71.68c{m^2}$
This is the required answer.

Note: In this type of question, first we have to know what is given and what we have to find in the question. Here we were asked the total surface area of a golf ball which is exposed to the surroundings . Here, we have found the total surface area of the ball and then we have removed the area occupied by the 150 dimplets each of given radius . we have removed only the $\pi {r^2}$ area of the dimplet as shown in the figure. Through this we got the answer.