Question

A hemispherical bowl is made of steel, 0.25cm thick. The inner radius of the bowl is 5cm. Find the outer curved surface area of the bowl.

Answer 1

Hint: Outer radius of a hollow hemisphere is the sum of the inner radius and the thickness.Outer curved surface area of a hollow hemisphere is $2\pi {r^2}$ where ‘r’ is the outer radius of the hemisphere and $'\pi '$ is equal to 22/7 or 3.14.

Complete step-by-step answer:

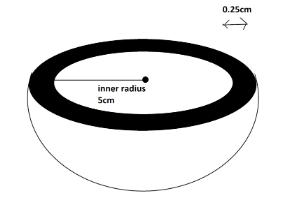
We are given that the hemispherical bowl is made of steel which has thickness 0.25cm and the inner radius of the bowl is 5cm.
Outer radius of the bowl = inner radius of the bowl + thickness of the bowl
$r_2 = r_1 + t$ , where ‘ $r_2$’ is the outer radius, ‘ $r_1$’ is the inner radius and t is the thickness.

$r_2 = 5+0.25$
$r_2 = 5.25$cm
We obtained the outer radius of the bowl.
Outer curved surface area of the bowl where outer radius is $r_2$= $2\pi{r_2}^2$
$
   = 2 \times \pi \times r_2 \times r_2 \\
   = 2 \times \dfrac{{22}}{7} \times 5.25 \times 5.25 \\
   = \dfrac{{2 \times 22 \times 5.25 \times 5.25}}{7} \\
   = \dfrac{{1212.75}}{7} \\
   = 173.25c{m^2} \\
 $
Outer curved surface area of the steel bowl with inner radius 5cm and thickness 0.25cm is 173.25 square centimeters.


Note: A hemisphere is defined as a three-dimensional shape that's half of a sphere with one flat, circular side. We can find various real-life examples of the hemispheres such as our planet Earth can be divided into two segments which are southern & northern hemispheres. The Hemispheres can either be of a solid type or can be hollow. Total Surface area of a hollow hemisphere is different from the total surface area of a solid hemisphere. Do not confuse a solid hemisphere with a hollow hemisphere. A hollow hemisphere has two radii i.e. inner radius and outer radius and two areas i.e. inner curved surface area and outer curved surface area.