Question

A hiker stands on the edge of a cliff of 490m, above the ground and throws a stone horizontally with an initial speed of $15m{{s}^{-1}}.$ Neglecting air resistance, find the time taken by the stone to reach the ground, and the speed with which it hits the ground. (Take g=$9.8m{{s}^{-2}}$)

Answer 1

Hint: The question is based on two dimensional kinematics. Knowing how to break speed and acceleration into horizontal and vertical components will help in solving this problem. Additionally, if you know formulas of various quantities such as height, velocity, acceleration etc. for two dimensional kinematics, it is helpful.

Step by step solution:
Let’s start off by making a diagram of the problem. We have a cliff of height 490m, from where a ball is thrown horizontally with velocity $15m{{s}^{-1}}.$ The gravity (g=$9.8m{{s}^{-2}}$) acts vertically downwards. This leads to the ball making a trajectory instead of following the straight path. We will consider the positive x axis as it moves from left to right and for y axis, positive is from top towards the bottom. Hence, g is positive.

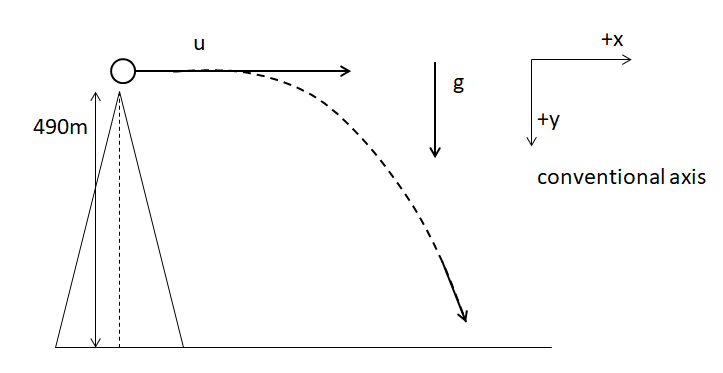
Hence, Vertical height$:h=y=490m.$ The initial velocity is only along the horizontal axis, hence, $u={{u}_{x}}=15m{{s}^{-1}}.$
Let’s use the formula for distance along the y axis, $y={{u}_{y}}t+\dfrac{1}{2}g{{t}^{2}}$.
Since, ${{u}_{y}}=0$ as no initial vertical velocity is given to the ball. Therefore, $490=0\times t+\dfrac{1}{2}(9.8){{t}^{2}}\Rightarrow 490=4.9{{t}^{2}}\Rightarrow 100={{t}^{2}}$
Therefore, $t=10\operatorname{s}.$
The final velocity of the particle along the y direction will be given by, $v_{y}^{2}-u_{y}^{2}=2gy$
Hence, $v_{y}^{2}-{{(0)}^{2}}=2(9.8)(490)\Rightarrow v_{y}^{2}={{98}^{2}}\Rightarrow {{v}_{y}}=98m{{s}^{-1}}$
The final velocity along the x axis (or) the horizontal direction is the same as the initial horizontal velocity as there is no acceleration along the x axis.
Therefore,${{v}_{x}}={{u}_{x}}=15m{{s}^{-1}}.$
Hence the final velocity will be $v=\sqrt{v_{x}^{2}+v_{y}^{2}}\Rightarrow v=\sqrt{{{98}^{2}}+{{15}^{2}}}=\sqrt{225+9604}=\sqrt{9829}\Rightarrow v=99.14m{{s}^{-1}}$
Hence, the ball will hit the ground with a velocity of $99.14m{{s}^{-1}}$ and the time of flight is 10s.

Note: An alternate way to find the final velocity along the vertical axis is using Newton's first law of motion. That is, $v=u+at$. This changes to ${{v}_{y}}={{u}_{y}}+{{a}_{y}}t$. Here initial velocity along vertical direction was already zero and hence, ${{v}_{y}}=0+9.8(10)\Rightarrow {{v}_{y}}=98m{{s}^{-1}}$ which is the same that we found earlier in the solution.
The time of flight will be the same that we found by using the y axis oriented variables as it would be, if we found out using the x axis oriented variables.