Question

A hollow cone is cut by a plane parallel to the base and the upper portion is
removed. If the curved surface of the remainder is $\dfrac{8}{9}$ of the curved surface of the whole cone, find the ratio of the line segments into which the cone’s altitude is divided by the plane.

Answer 1

Hint: This is a problem of mensuration and requires the concept of volumes of 3-D objects. We assume two variables for the length of the two-line segments and form the equation using the given information. The curved surface area of the hollow cone is-
$CSA = \pi rl$ where r is the radius and l is the slant height of the cone…………..(1)

Complete step-by-step solution -

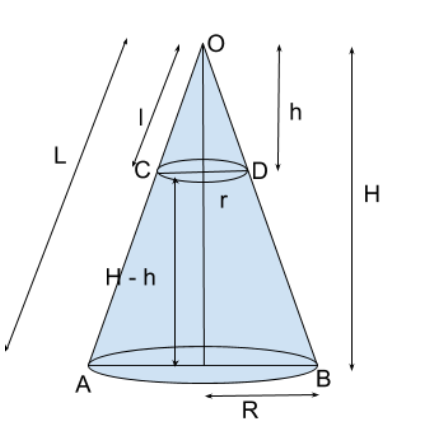
Let the cone OAB of radius R, height H, and slant height L, be cut horizontally across CD. Let the smaller cone OCD thus formed have radius r, height h, and slant height l. We will first try to find the relation between r, h, l and R, H, L as-
$\begin{align}
  &In\;\vartriangle OCD\;and\;\vartriangle OAB, \\
  &\angle COD = \angle AOB\left( {common} \right) \\
  &\angle OCD = \angle OAB\left( \text{corresponding angles of parallel lines CD, and AB} \right) \\
 &\text{By AA similarity,} \\
 &\vartriangle OCD\text{~}\vartriangle OAB \\
\end{align} $
We know that the corresponding sides and altitudes of similar triangles are proportional to each other. So, we can write that-
$\begin{align}
 \Rightarrow &\dfrac{{OC}}{{OA}} = \dfrac{{CD}}{{AB}} \\
 \Rightarrow &\text{From figure we can write that} - \\
 \Rightarrow &\dfrac{{\text{l}}}{{\text{L}}} = \dfrac{{2{\text{r}}}}{{2{\text{R}}}} = \dfrac{{\text{r}}}{{\text{R}}} \\
\end{align} $

We know that h and H are the altitudes of the two triangles OCD and OAB respectively, so-
$\dfrac{{\text{l}}}{{\text{L}}} = \dfrac{{\text{r}}}{{\text{R}}} =
\dfrac{{\text{h}}}{{\text{H}}}..................(2)$

Now, we have been given that the curved surface of the remainder is $\dfrac{8}{9}$ of the curved of the surface of the whole cone so-
$\begin{align}
 &\text{CSA of whole cone OAB} = \pi RL = {{\text{C}}_1} \\
&\text{CSA of leftover portion} = \text{ CSA of cone OAB - CSA of cone OCD} = {{\text{C}}_2}\\
  &{{\text{C}}_2} = \pi RL - \pi rl \\
\end{align} $
We know that-
$\begin{align}
\Rightarrow &\dfrac{{{{\text{C}}_2}}}{{{{\text{C}}_1}}} = \dfrac{8}{9} \\
 \Rightarrow &\dfrac{{\pi RL - \pi rl}}{{\pi RL}} = \dfrac{8}{9} \\
 \Rightarrow &\dfrac{{RL - rl}}{{RL}} = \dfrac{8}{9} \\
 \Rightarrow &9RL - 9rl = 8RL \\
 \Rightarrow &RL = 9rl \\
 \Rightarrow &\dfrac{{\text{R}}}{{\text{r}}} = 9\left( {\dfrac{{\text{l}}}{{\text{L}}}} \right) \\
\end{align} $
From equation (2) we can write that-
$\begin{align}
  &\dfrac{{\text{R}}}{{\text{r}}} = 9\left( {\dfrac{{\text{r}}}{{\text{R}}}} \right) \\
\Rightarrow &{\left( {\dfrac{{\text{R}}}{{\text{r}}}} \right)^2} = 9 \\
 \Rightarrow &\dfrac{{\text{R}}}{{\text{r}}} = 3 \\
 \Rightarrow &{\text{R}} = 3{\text{r}} \\
\end{align} $
From equation (2), we know that-
$\begin{align}
  &\dfrac{{\text{r}}}{{\text{R}}} = \dfrac{{\text{h}}}{{\text{H}}} \\
 \Rightarrow &\dfrac{{\text{h}}}{{\text{H}}} = \dfrac{{\text{r}}}{{3{\text{r}}}} = \dfrac{1}{3} \\
\end{align} $
But this is not the final answer. We have to find the ratio of the two line segments into which the cone’s altitude is divided. The two lines segments are h and (H - h), so we need to find-
$h : (H - h)$
$\dfrac{{\text{h}}}{{{\text{H}} - {\text{h}}}} = \dfrac{{\text{h}}}{{3{\text{h}} - {\text{h}}}} = \dfrac{{\text{h}}}{{2{\text{h}}}} = \dfrac{1}{2}$
Hence, the ratio is $1 : 2$
This is the required answer.

Note: This is a complex problem involving a number of concepts. We should remember the formulas of the curved surface area of the cone, the rules of similarity of triangles as well as ratio and proportions. The most common mistake which is done is that the students leave the question after finding the ratio of heights of the cones and write the answer as $1:3$. This is a wrong answer because we need to find the ratio of the two-line segments which are formed after dividing H.