Question

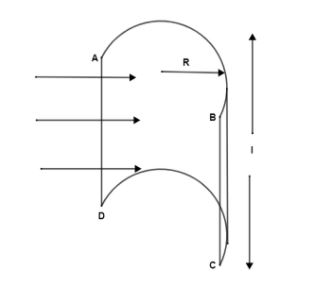
A hollow half cylinder surface of radius R and length l is placed in a uniform electric field E. Electric Field is acting perpendicular on the ABCD. If the flux through the curved surface of the hollow cylindrical surface is $E\times XRl$. Find X.

Answer 1

Hint: We will take the help of the formula of electric flux in order to solve the question. This is because the electric field lines are passing through the rectangular side of the hollow cylinder. So, with the help of electric flux we will be able to use both electric fields and the area as a product.

Formula used: $\phi =E\times A$ where the area through which the electric field lines passes is represented as A and the electrical field is denoted by E. The area of the rectangle ABCD = (AB)(BC).

Complete step-by-step answer:
Electrical Field: In simple terms we can define the electric field as an electrical property in which the field lines which form after any two charged particles contact. The two charged particles either come in contact or repel according to the charges on them. Take for example we take two positively charged particles which will repel each other after forming electrical fields after contact.
The SI unit of the electric field is Volts per meter (V/m).
It is always a vector quantity as it is judged on the basis of its direction and magnitude both.
Electric flux: By the term electric flux we mean the number of lines of a field that are successful at passing through an area denoted by A. The SI unit of electric flux id Volt meters. This can be easily understood by the following diagram.

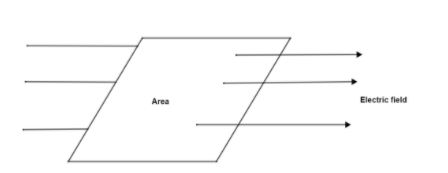
Here, the electric flux can be calculated by using the product of the area through which the electric field lines pass (represented as A) and the electrical field (denoted by E). Numerically, we can write it as $\phi =E\times A$.
The electric field lines passing through the rectangular part of the hollow cylinder gives the electric flux as the product of the electric field and the area of the rectangle ABCD which is given in the question. According to the diagram given in the question, the area of the rectangle ABCD = (AB) (CD). As, R is the radius and AB represents the diameter so the value of AB will be 2 times radius. Also, since BC is represented as a length of l so, the flus is calculated as,
$\phi =E\times \left( AB\times BC \right)$
$\Rightarrow \phi =E\times \left( 2R\times l \right)$…(i)
Since, we are given that the flux is $\phi =E\times XRl$…(ii) so, by the equations (i) and (ii) we get X = 2.
Hence, the value of X is 2 resulting in a hollow half cylinder surface of radius R and length l is placed in a uniform electric field E with Electric Field acting perpendicular on the ABCD. If the flux through the curved surface of the hollow cylindrical surface is $\phi =E\times \left( 2R\times l \right)$.

Note: The things to be on your finger tips for further questions like this are,
(1) The definition of electric field.
(2) The definition and formula of electric flux: $\phi =E\times A$
(3) The SI unit of the electric field is Volts per meter (V/m).
(4) The SI unit of electric flux id Volt meters.