Question

A hollow insulated conducting sphere is given a positive charge of $10\mu C$ . What will be the electric field at the center of the sphere if its radius is 2 meters?
$\begin{align}
  & (a)Zero \\
 & (b)5\mu C{{m}^{-2}} \\
 & (c)20\mu C{{m}^{-2}} \\
 & (d)8\mu C{{m}^{-2}} \\
\end{align}$

Answer 1

Hint: We shall use the Gauss law to find the net field due to the positive charge inside the insulated conducting sphere. Gauss law is stated as, the total Electric flux through a uniformly enclosed surface is equal to the total charge inside the surface divided by its permittivity of space.

Complete answer:
Let us first understand that, since the positive charge is given to a conducting hollow sphere, the charge will remain at the outer surface of the sphere and not in its volume. This is understood by the following diagram:
       

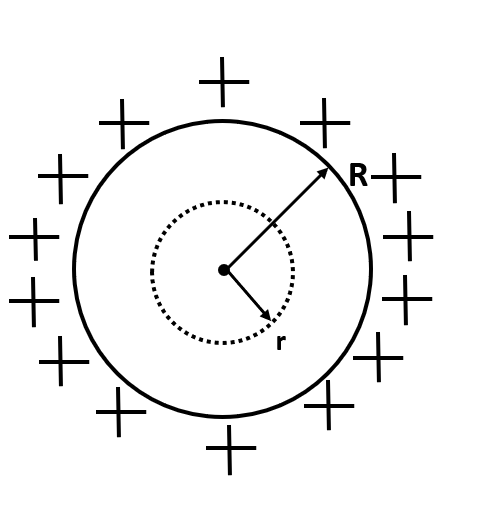
Here, we can see that the charge given to the sphere is uniformly distributed over its entire surface area only and not over its volume inside.
To calculate the electric field inside, we apply the Gauss theorem. Let us take a sphere of radius $r$ with the same center as the larger sphere, where $r$ is less than $R$ .
Then, for this imaginary uniform surface, the Gauss equation will be:
$\Rightarrow \int E.ds=\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
Since we know that the charge inside the hollow spherical conductor is zero. Therefore we can write the above equation as:
$\begin{align}
  & \Rightarrow \int E.ds=0 \\
 & \Rightarrow E=0 \\
\end{align}$
This means for different values of $(r)$ , the electric field inside the sphere is zero everywhere.
Hence, the electric field at the center of the sphere is also equal to zero.

Thus, option (a) is the correct option.

Note:
In this problem, we saw that the data given in the problem had nothing to do with the actual solution. So, we need to be careful as these data sets are only to confuse one. We should be very well aware of these concepts as they form a very important part of Electrostatics.