
A house is built on the top of a hill with \[45^\circ \]slope. Due to the sliding of material and sand from top to the bottom of the hill, the slope angle has been reduced. If the coefficient of static friction between sand particles is 0.75, what is the final angle obtained by hill? (${\tan ^{ - 1}}0.75 = 37^\circ $ ).
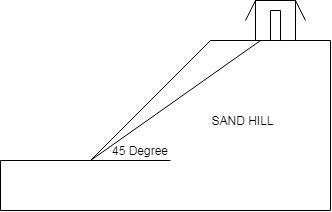
A) $8^\circ $
B) $45^\circ $
C) $37^\circ $
D) $30^\circ $
Answer
233.1k+ views
Hint: Here we have to use the concept of resolution of forces. Here, we need to find the equilibrium of the sand. So to do that we need to find equations for all the forces so that the net forces are equal to zero.
Complete step by step solution:
Resolve forces and find the angle:
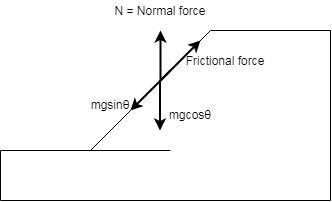
Resolve the vertical and the horizontal forces,
$N = mg\cos \theta $; …(m = mass, g = acceleration due to gravity)
Now, resolve the horizontal forces equate them together.
$\mu N = mg\sin \theta $; …(Frictional force = $\mu N$)
Put the value of N in the above equation:
$\mu \times mg\cos \theta = mg\sin \theta $;
Solve for the coefficient of friction and cancel out the terms with same values.
$\mu = \dfrac{{mg\sin \theta }}{{mg\cos \theta }}$;
$\mu = \tan \theta $;
Solve for the angle;
${\tan ^{ - 1}}\mu = \theta $;
Put the value of coefficient of friction which is 0.75.
${\tan ^{ - 1}}0.75 = \theta $;
The angle is:
$\theta = 37^\circ $;
Hence, Option (C) is correct. The final angle attained by the hill is $37^\circ $.
Note: Here the sand is sliding that means the forces on the sand are not in equilibrium. When the sand stops sliding that means the net force on the sand is equal to zero. Here, draw a diagram specifying each of the forces acting on the sand. Find the unknown angle.
Complete step by step solution:
Resolve forces and find the angle:

Resolve the vertical and the horizontal forces,
$N = mg\cos \theta $; …(m = mass, g = acceleration due to gravity)
Now, resolve the horizontal forces equate them together.
$\mu N = mg\sin \theta $; …(Frictional force = $\mu N$)
Put the value of N in the above equation:
$\mu \times mg\cos \theta = mg\sin \theta $;
Solve for the coefficient of friction and cancel out the terms with same values.
$\mu = \dfrac{{mg\sin \theta }}{{mg\cos \theta }}$;
$\mu = \tan \theta $;
Solve for the angle;
${\tan ^{ - 1}}\mu = \theta $;
Put the value of coefficient of friction which is 0.75.
${\tan ^{ - 1}}0.75 = \theta $;
The angle is:
$\theta = 37^\circ $;
Hence, Option (C) is correct. The final angle attained by the hill is $37^\circ $.
Note: Here the sand is sliding that means the forces on the sand are not in equilibrium. When the sand stops sliding that means the net force on the sand is equal to zero. Here, draw a diagram specifying each of the forces acting on the sand. Find the unknown angle.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




