Question

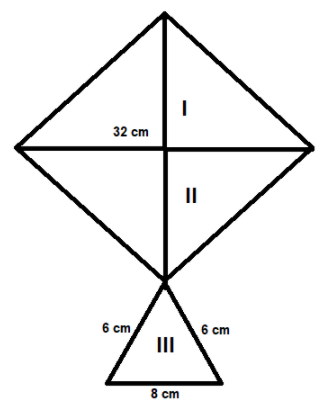
A kite in the shape of a square with diagonal 32 cm and isosceles triangle with base 8 cm and sides 6 cm each is to be made of three different shades. How much paper of each shade has been used ?

Answer 1

Hint:
We are asked to make a kite with three shades of paper and the kite kite is made with a square of diagonal 32 cm and a isosceles triangle with base 8 cm and sides 6 cm . we can find the area of the square portion using the formula $\dfrac{1}{2}{d^2}$and dividing it by 2 we get the amount of paper used to make portion I and II and the amount of paper used to make the III portions is found by using the herons formula $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ where a , b , c are the sides of the triangle and s is the half of the perimeter of the triangle.

Complete step by step solution:
We are given a kite and said that it is made up of three different shades of paper
The kite is made of a square and a triangle

We are given that the square has a diagonal which 32 cm
With this we can find the area of the square portion
When a diagonal of the square is given its area is given by $\dfrac{1}{2}{d^2}$
Hence the area of the square portion is given as
$
   \Rightarrow \dfrac{1}{2}\times {\left( {32} \right)^2} \\
   \Rightarrow \dfrac{1}{2}\times 1024 \\
   \Rightarrow 512c{m^2} \\
 $
Now this square portion is made with two shades of paper
And we know that the diagonal of a square splits it into two tringles of equal areas
Hence amount of paper used to make portion I is equal to the amount of paper used to make potion II
So from this we get that the area of the square is twice the area of portion I or II
Therefore the amount of paper used to make portion I is $\dfrac{{512}}{2} = 256c{m^2}$
And the amount of paper used to make portion II is $\dfrac{{512}}{2} = 256c{m^2}$
And we are given that the third portion is made of an isosceles triangle with base 8 cm and sides 6 cm
We can find the area of the triangle when sides are given by using heron’s formula
$ \Rightarrow Area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Where a , b , c are the sides of the triangle and s is the half of the perimeter of the triangle
We can find the perimeter by adding up the sides
$ \Rightarrow s = \dfrac{{Perimeter}}{2} = \dfrac{{8 + 6 + 6}}{2} = \dfrac{{20}}{2} = 10cm$
Hence using the known values in the heron's formula we can get the amount of paper used to make portion III
$
   \Rightarrow Area = \sqrt {10\left( {10 - 8} \right)\left( {10 - 6} \right)\left( {10 - 6} \right)} \\
   \Rightarrow Area = \sqrt {10\left( 2 \right)\left( 4 \right)\left( 4 \right)} \\
   \Rightarrow Area = \sqrt {\left( {20} \right)\left( {16} \right)} = \sqrt {64\times 5} \\
   \Rightarrow Area = 8\sqrt 5 = 8(2.236) = 17.89c{m^2} \\
 $

Hence we obtained the amount of paper used to make portion III.

Note:
1) Here we use heron’s formula to find the area of the triangle as we are not given the height of the triangle
2) the area can be defined as the space occupied by a flat shape or the surface of an object.
3) The area of a figure is the number of unit squares that cover the surface of a closed figure. Area is measured in square units such as square centimeters, square feet, square inches, etc