Question

A LCR circuit behaves like a damped oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant ‘b’, the correct equivalence would be:
A. $L \leftrightarrow m,C \leftrightarrow k,R \leftrightarrow b$
B. $L \leftrightarrow \dfrac{1}{b},C \leftrightarrow \dfrac{1}{m},R \leftrightarrow \dfrac{1}{k}$
C. $L \leftrightarrow k,C \leftrightarrow b,R \leftrightarrow m$
D. $L \leftrightarrow m,C \leftrightarrow \dfrac{1}{k},R \leftrightarrow b$

Answer 1

Hint: To solve this question, we have to solve damping equations for both LCR and spring-mass systems. Then we have to find the analogy in the equations. Comparing them will give us the correct result.
For spring-mass system
 \[m\dfrac{{{d^2}x}}{{d{t^2}}} + b\dfrac{{dx}}{{dt}} + kx = 0 - - - (1)\]
For LCR system
 $L\dfrac{{{d^2}q}}{{d{t^2}}} + R\dfrac{{dq}}{{dt}} + \dfrac{q}{c} = 0 - - - (2)$
Find analogy in equation (1) & (2), you will get the answer

Complete step-by-step solution:

We know in spring-mass balance system some velocity is initially given, and damping force always oppose the motion so
Damping force ${F_D} \propto v$
  ${F_D} = - bv - - - (3)$
Where ${F_D}$ is damping force, $b$ is proportionality constant, $v$is velocity and negative sign is to show that damping force opposes the motion.
Force by spring, according to hooke's law ${F_s} \propto x$
${F_s} = - kx - - - (4)$
Where, ${F_s} = $ force by spring
$k = $ spring constant
$x = $ value of displacement from origin
Negative is also there as, spring force also oppose the motion
So, net force
 ${F_{net}} = {F_D} + {F_s}$
On putting values from equation (3) & (4)
 ${F_{net}} = - bv - kx$
According to newton’s second law of motion, net force is mass times acceleration
$ma = - bv - kx$
$ \Rightarrow ma + bv + kx = 0 - - - (5)$
Where $m = $ mass and $a = $ acceleration
Converting equation (5) into differential form
\[m\dfrac{{{d^2}x}}{{d{t^2}}} + b\dfrac{{dx}}{{dt}} + kx = 0 - - - (6)\] $\left[ {\because a = \dfrac{{dv}}{{dt}},v = \dfrac{{dx}}{{dt}}} \right]$
In LCR circuit

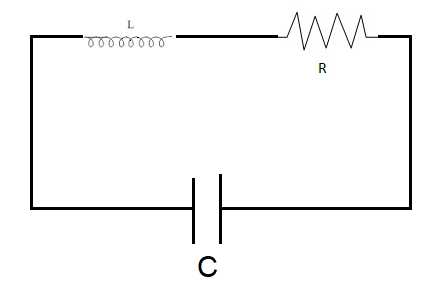
Here in figure ‘R’ is resistance of resistor, ‘L’ is inductance of inductor and ‘C’ is capacitance of capacitor.
Applying kirchhoff's loop law or kirchhoff's voltage law, according to the law if you traverse throughout the circuit then net voltage sum will be zero.
 $\therefore - IR - L\dfrac{{dI}}{{dt}} - \dfrac{q}{C} = 0 - - - (7)$ $\left[ {\because {V_r} = IR,{V_L} = L\dfrac{{dI}}{{dt}},{V_c} = \dfrac{q}{c}} \right]$
Where \[{V_r} = \] voltage across resistor, \[{V_c} = \] voltage across capacitor, ${V_L} = $ voltage across inductor and $I = $ current flowing through circuit
On further solving the equation (7)
 $L\dfrac{{{d^2}q}}{{d{t^2}}} + R\dfrac{{dq}}{{dt}} + \dfrac{q}{C} = 0 - - - (8)$
Comparing equations (6) & (7)
We get
 $L \leftrightarrow m,C \leftrightarrow \dfrac{1}{k},R \leftrightarrow b$
Therefore option (D) is the correct answer.

Note:-
Kirchoff’s first law or Kirchoff’s circuital law states that the algebraic sum of current leave and entering at a node is always equal to zero.
In a differential equation, the number of arbitrary constants is equal to the order of the differential equation. There are various standard results for different kinds of complex differential equations, remembering them can be handy in examination.