Question

A leakage begins in the water tank at position P as shown in the figure. The initial gauge pressure at P was $5 \times {10^5}N/{m^2}$ .if the density of water is $1000kg/{m^3}$ the initial velocity with which water gushes out is:
     

A) $3.2m/\sec $
B) $32m/\sec $
C) $28m/\sec $
D) $2.8m/\sec $

Answer 1

Hint:
To solve this question we use Bernoulli’s theorem which is ${P_1} + \dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2}$
And we know the gauge pressure is pressure above that of the atmospheric pressure at that point can be represented as $P - {P_{atm}} = \rho gh$ .
Where $P \Rightarrow $ is the total pressure at that point or at that level

Step by step solution:
First we mark another point Q at the same level of P let as assume the point P and Q are $h$ height below the free surface of the water tank.
As shown in figure.
     

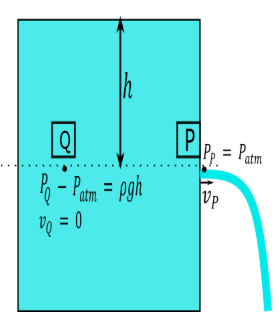
From figure we can write the gauge pressure at point Q is ${P_Q} - {P_{atm}} = \rho gh$
Where $\rho \Rightarrow $ density of water
${P_Q} \Rightarrow $ Total pressure at point Q
$h \Rightarrow $ Height from free surface
So from this we can Wright the pressure at point Q is
$ \Rightarrow {P_Q} = {P_{atm}} + \rho gh$ ......... (1)
Pressure at point P is equal to the atmospheric pressure
 ${P_P} = {P_{atm}}$ ......... (2)
Velocity at point Q is approximately equal to zero
 ${v_Q} = 0$....... (3)
Let us assume the velocity at point P is with which water comes out is ${v_P}$
Step 2
Now we apply Bernoulli’s theorem for horizontal points P and Q.
$ \Rightarrow {P_P} + \dfrac{1}{2}\rho {v_P}^2 + \rho g{h_P} = {P_Q} + \dfrac{1}{2}\rho {v_Q}^2 + \rho g{h_Q}$
Because point P and Q are at same horizontal level ${h_P} = {h_Q}$ so Bernoulli theorem reduced to
$ \Rightarrow {P_P} + \dfrac{1}{2}\rho {v_P}^2 = {P_Q} + \dfrac{1}{2}\rho {v_Q}^2$
Put all values in this equation from (1) (2) and (3)
\[ \Rightarrow {P_{atm}} + \dfrac{1}{2}\rho {v_P}^2 = \left( {{P_{atm}} + \rho gh} \right) + \dfrac{1}{2}\rho {\left( 0 \right)^2}\]
\[ \Rightarrow \dfrac{1}{2}\rho {v_P}^2 = \rho gh\]
Now ${P_Q} - {P_{atm}} = \rho gh = 5 \times {10^5}N/{m^2}$ given in question
Put $\rho gh = 5 \times {10^5}$ and density of water $\rho = 1000kg/{m^3}$
\[ \Rightarrow \dfrac{1}{2} \times 1000 \times {v_P}^2 = 5 \times {10^5}\]
\[ \Rightarrow {v_P}^2 = \dfrac{{5 \times {{10}^5} \times 2}}{{1000}}\]
Further solving
\[ \Rightarrow {v_P} = \sqrt {\dfrac{{5 \times {{10}^5} \times 2}}{{1000}}} \]
\[ \Rightarrow {v_P} = \sqrt {1000} \]
\[ \Rightarrow {v_P} = 31.62m/\sec \]
Hence the velocity to exit the water tank at point P is approximately $32m/\sec $

therefore Option B is correct

Note:
We can solve this question by another short method which is given below
We know gauge pressure $P = \rho gh$ from this we can find height of hole from free surface
$
   \Rightarrow 5 \times {10^5} = 1000 \times 10 \times h \\
   \Rightarrow h = 50m \\
 $
And now apply Torricelli’s theorem formula velocity of Efflux $v = \sqrt {2gh} $
$
   \Rightarrow v = \sqrt {2 \times 10 \times 50} \\
   \Rightarrow v = \sqrt {1000} \\
  \therefore v = 31.62m/\sec \\
 $