Question

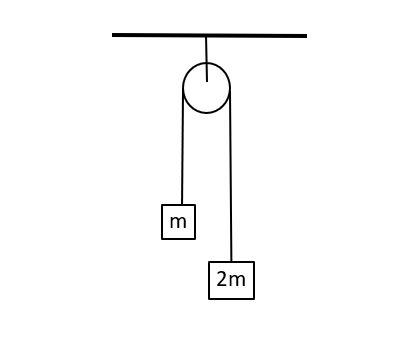
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36kg and 0.72kg. Taking $g=10m/s^2$, find the work done (in joules) by the string on the block of mass 0.36kg during the first second after the system is released from rest.

Answer 1

Hint: Let us first draw the free body diagram of the given system of blocks. Then we can find the tension in the string and the acceleration with which both the masses will ascend or descend. Then the actual work done will be due to the tension on the smaller block and thus using the equation of motion, we will calculate the height ascended by the block in the first second. And then the work done can be calculated using its formula.

Formulae used:
Distance, $s=ut+\dfrac{1}{2}at^2$
Work done, w = Force $\times$ Displacement

Complete step by step solution:
We have been given that two blocks of masses $m=0.36kg$ and $2m=0.72kg$ has been attached with a light inextensible string.
Let us first draw the free body diagram for the given system,

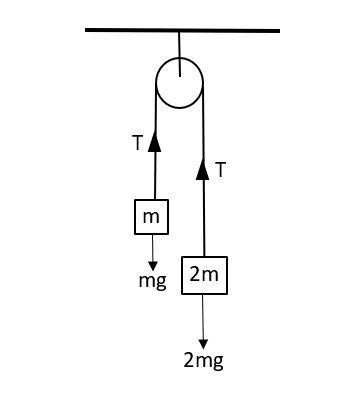
The two blocks will experience their weights and a tension T will develop in the string as the block with mass $2m$ will start to descend.
Let the two blocks start to move with acceleration $a$ after they are left from rest.
We can write for blocks with mass $m$, $T-mg=ma$ ………. (i)
And for block of mass $2m$, $2mg-T=2ma$ ………. (ii)
Adding equations (i) and (ii), we get
$mg=3ma\implies a=\dfrac{g}{3}$
Substituting this in the equation (i) to get the value of tension,
$T-mg=\dfrac{mg}{3}=\dfrac{4mg}{3}$
Now, we need to find the height ascended by the block of mass $m$ in one second as it starts from rest with an acceleration $a$,
$s=\dfrac{at^2}{2}=\dfrac{g}{6}$
So, the work done by the block, will be due to the tension acting on it as the motion is because of the tension,
So, work done $w=T\times s =\dfrac{4mg}{3}\dfrac{g}{6}=\dfrac{4\times 0.36\times 10^2}{18}=8$ Joules.
Hence, work done by the block of mass 0.36kg in the first second will be 8 Joules.

Note: We can also find the work done by the block from its change in state of energy. After the first second, the block will ascend some height and thus will gain both kinetic and potential energy and we know that work done is the change in energy of a system per unit time.