Question

A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of mass 0.36kg and 0.72kg. Taking $g=10ms^{-2}$, find the work done (in Joules) on the block of mass 0.36kg by the string during the first second after the system is released from rest.
A. 6 Joules
B. 2 Joules
C. 5 Joules
D. 8 Joules

Answer 1

Hint: Since the weight on both sides is not equal, hence one side will exert more force to result in a motion. In the question, it is given that the system starts from rest. Hence the tension in the string will exert force and displace the blocks. Hence some work will be done by the string to result in the kinetic energy of the blocks.

Formula used:
$s = ut + \dfrac 12 at^2, \ W = F.s, \ a_{net} = \dfrac{Net \ pulling \ force}{Total \ mass \ of \ the \ system}$

Complete step by step answer:
First of all, for getting the acceleration of the blocks, we need to get net pulling force which is the difference in the weights of both the blocks.
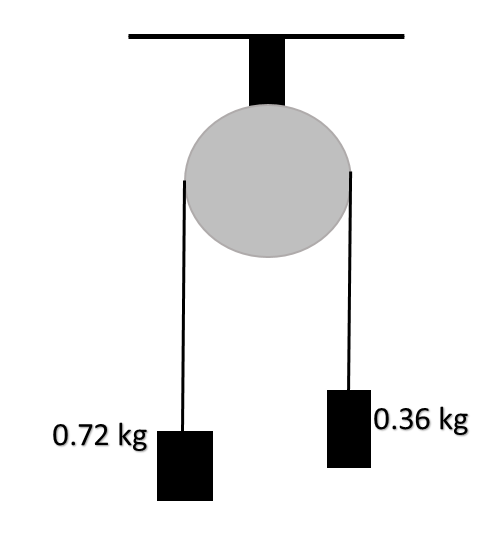
Hence, net pulling force = $W_1 - W_2 = m_1 g - m_2 g = 0.72 \times g - 0.36 \times g = 0.72 \times 10 - 0.36 \times 10 = 7.2 - 3.6 = 3.6 N$
Now, total mass of the system = $m_1 + m_2 = 0.72 + 0.36 = 1.08 kg$
Hence the acceleration of the blocks (magnitude) $a_{net} = \dfrac{Net \ pulling \ force}{Total \ mass \ of \ the \ system} = \dfrac{3.6}{1.08} = 3.33 ms^{-2}$
Now, as we need the work done on 0.36 kg block, hence we will find the force (F) on block:
$F = ma$
$F = 0.36 \times 3.33 = 1.2 N$
Now, using equation $s = ut + \dfrac 12 at^2$, to get the displacement of block in first second, we have;
u=0 [as system is started from rest]
$a=3.33 ms^{-2}$
t=1 sec
Hence,$s = 0\times 1 + \dfrac 12 3.33 \times 1^2 = \dfrac 53 m$
Now, using $W = F.s$
F = 1.2 N
$s=\dfrac 53 m$
Hence, $W = 1.2 \times \dfrac 53 = 2 J$
Hence the work done is 2 Joules, option B. is correct.

Note:
One can also proceed by drawing the free body diagrams of the blocks but this will take more time for solving. Students are advised to learn and understand this formula for finding the net acceleration of the blocks. This acceleration has the magnitude given by the formula and the direction of the acceleration is towards the block of greater mass.