Question

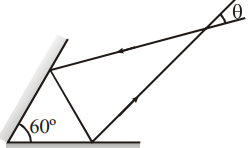
A light ray is incident on a plane mirror, which after getting reflected strikes another plane mirror, as shown in figure. The angle between the two mirrors is $60^{\circ}$. Find the angle $\theta$ is shown in figure.

Answer 1

Hint : In this question, we will use angle sum property. A triangle containing three angles and three sides and a pair of neighbouring sides bound each vertex. In a Euclidean period, the sum of triangle angles equals $180$ degrees. It does not matter if the triangle is obtuse, an acute, or a right triangle; the sum of all angles will be $180$ degrees. Thus, the angle sum property says that the sum of the triangle angles is equal to $180$ degrees.

Complete step-by-step solution:
The angle between the two mirrors is $60^{\circ}$.
Let $\angle A =2x$
$\angle B =2y$
This gives,
$\angle OAB =90^{\circ} - x$
$\angle OBA =90^{\circ} - y$

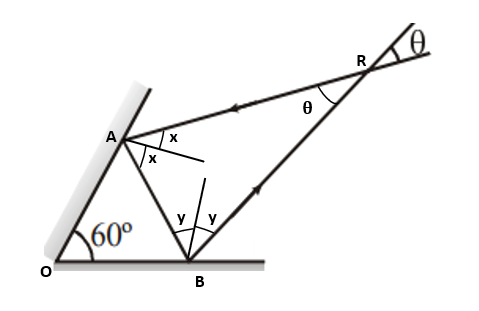
In triangle OAB,
Using sum of angle property,
$60^{\circ} + (90^{\circ} - x) +(90^{\circ} - y) = 180^{\circ} $
$\implies 60^{\circ} -x -y = 0$
$\implies x + y = 60^{\circ} $
Now, we will apply sum of angle property,
$\theta + 2x + 2y = 180^{\circ} $
Put $ x + y = 60^{\circ} $ in above formula:
$\theta + 2 (60^{\circ}) = 180^{\circ}$
$\implies \theta = 180 – 120 = 60^{\circ} $
Hence, the angle $\theta$ is $60^{\circ}$.

Note: A mirror is a reflective covering that light does not move through but bounces off, producing an image. Mirrors are formed by putting a thin coating of silver nitrate or aluminium following a smooth piece of glass. When we place an object in the face of a mirror, we see the identical object in the mirror.