Question

A line L passing through the focus of the parabola ${{y}^{2}}=4\left( x-1 \right)$, intersects the parabola in two distinct points. If ‘m’ be the slope of the line ‘L’ then
(A) -1 < m < 1
(B) m< -1 or m > 1
(C) $m\in R$
(D) None of the above

Answer 1

Hint: Focus of parabola with equation ${{y}^{2}}=4\left( x-1 \right)$is (a, 0). Quadratic $A{{x}^{2}}+Bx+C=0$have real roots if ${{B}^{2}}=4AC=$Discriminant is greater than zero.

Complete step-by-step answer:
The given equation of parabola is
${{y}^{2}}=4\left( x-1 \right)............\left( 1 \right)$
As we know, the standard equation of parabola is ${{y}^{2}}=4ax$ with vertex (0, 0) and focus (a, 0). We can write the standard equation as ${{\left( y-0 \right)}^{2}}=4a\left( x-0 \right)$. Now, generalizing the above relation, we can rewrite parabola equation as ${{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)$ where $\left( {{x}_{1}}-{{y}_{1}} \right)$are vertex of the parabola and focus will shift to $\left( a+{{x}_{1}},{{y}_{1}} \right)$.
Now, comparing equation ${{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)$ with the given parabola equation (1) i.e. \[{{y}^{2}}=4\left( x-1 \right)or{{\left( y-0 \right)}^{2}}=4\left( x-1 \right)\], we get;
Vertex $=\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,0 \right)$
Focus $=\left( 1+1,0 \right)=\left( 2,0 \right)$
We can show vertex and focus of given parabola in diagram given below;

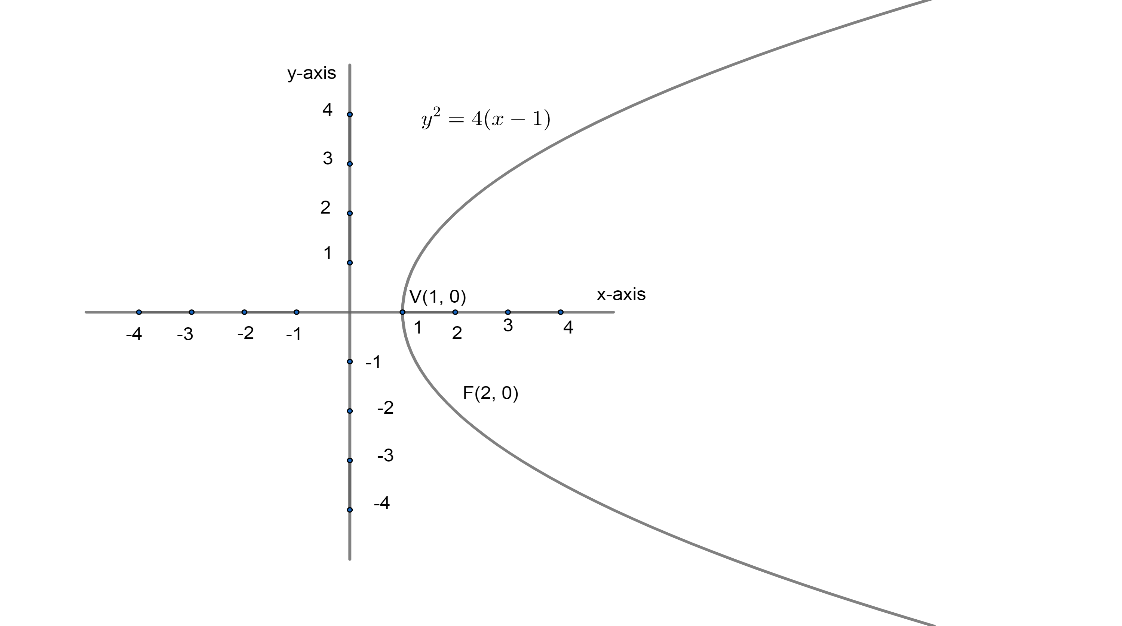
Now, we have line L passing through focus and intersecting the given parabola at two points.
Let us suppose line L as
$y=mx+c......\left( 2 \right)$
Where m is the slope of the line and c is the intercept on y-axis.
As, equation (2) is passing through focus (2, 0). Hence, it will satisfy the equation (2),
$\begin{align}
  & 0=2m+c \\
 & c=-2m..........\left( 3 \right) \\
\end{align}$
Now, equation (2) can be rewritten in variable ‘m’ as
$y=mx-2m...............\left( 4 \right)$
As we are given that equation (4) is intersecting at two points with the given parabola as expressed equation (1).
Now, for getting intersecting points, we can substitute ‘y’ from equation (4) to equation (1) i.e.${{y}^{2}}=4\left( x-1 \right)$. Hence, we get
${{\left( mx-2m \right)}^{2}}=4\left( x-1 \right)$
Simplifying \[{{\left( mx-2m \right)}^{2}}\] by using algebraic identity \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\], we get
\[\begin{align}
  & {{m}^{2}}{{x}^{2}}+4{{m}^{2}}-4{{m}^{2}}x=4x-4 \\
 & Or \\
 & {{m}^{2}}{{x}^{2}}-x(4{{m}^{2}}+4)+4{{m}^{2}}+4=0..........\left( 5 \right) \\
\end{align}\]
As the above equation is a quadratic equation in ‘x’, so we will get two roots of equation (5) which are x-coordinates of both the intersecting points of line ‘L’ with the given parabola.
As both the roots should be real.
Now, we know that any quadratic $A{{x}^{2}}+Bx+C=0$will have both roots real, if discriminant or $D={{b}^{2}}-4ac$ is greater than zero.
Hence, equation (5) has both roots real so discriminant of it should be greater than 0. Hence, we get,
$\begin{align}
  & {{\left( 4{{m}^{2}}+4 \right)}^{2}}-4{{m}^{2}}\left( 4{{m}^{2}}+4 \right)>0 \\
 & Or \\
 & 16{{m}^{4}}+16+64{{m}^{2}}-16{{m}^{4}}-16{{m}^{2}}>0 \\
\end{align}$
On simplifying the above relation, we get,
$48{{m}^{2}}+16>0..........\left( 6 \right)$
Now, we can observe that $48{{m}^{2}}+16$ will always be greater than zero for any real value of ‘m’. ${{m}^{2}}$will never be negative, for any real value of ‘m’. Hence, $m\in R$ is the condition for the given question that line ‘L’ always passes through two points if it passes through focus of given parabola.
Hence, option (C) is the correct answer.

Note: One can go wrong while writing the focus of the parabola of a given equation. He/she may take (1, 0) as focus of the given parabola. But it will be wrong and need to compare with ${{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)$ where vertex is $\left( {{x}_{1}},{{y}_{1}} \right)$and focus is $\left( {{x}_{1}}+a,{{y}_{1}} \right)$.
Hence, be careful while writing focus or vertex in these kinds of questions.
Another approach for this question would be that we can suppose two parametric coordinates on the given parabola as, \[\left( t_{1}^{2}+1,2{{t}_{1}} \right)\ and\ \left( t_{2}^{2}+1,2{{t}_{2}} \right)\]. A line is passing through (2,0) as well.
Hence, three points are collinear. Now, we know that if $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)\ and\ \left( {{x}_{3}},{{y}_{3}} \right)$ are collinear then triangle formed by all three points have area 0. Hence,
$\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|=0$
And slope can be given as $\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{t_{2}^{2}-t_{1}^{2}}$ which is equal to m. Now, using both the equations, try to get a relation between ‘m’.