Question

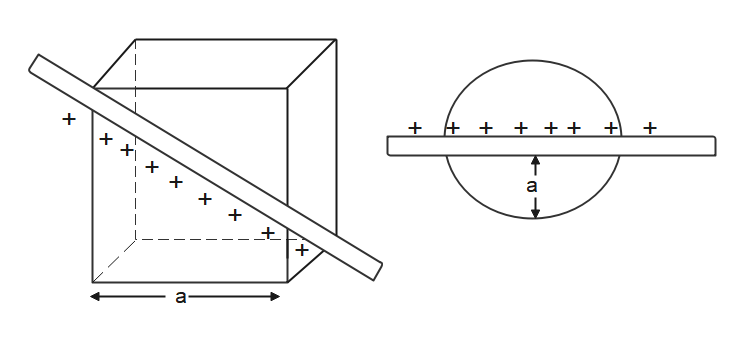
A linear charge having linear charge density $\lambda $ , penetrates a cube diagonally and then it penetrates a sphere diametrically as shown. What will be the ratio of flux coming out of the cube and sphere?

A)$\dfrac{1}{2}$
B)$\dfrac{2}{\sqrt{3}}$
C)$\dfrac{\sqrt{3}}{2}$
D)$\dfrac{1}{1}$

Answer 1

Hint: Coulomb's law deals with charges if the polarities of charges are the same then a repulsive force is created if the charges have different polarities then an attractive force is created. Coulomb’s law is an inverse square law; this law is analogous to Isaac Newton's inverse –square law of universal gravitation.

Formula Used:
$I=\dfrac{{E}/{V}\;}{R}$
Where, I is the amount of current flowing through the circuit,${E}/{V}\;$is defined as the amount of voltage drop in the whole circuit and R is the amount of resistance to be offered by the resistor in the circuit.

Complete step-by-step solution:
Coulomb’s law states that the magnitude of electrostatic force between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them
$\left| F \right|=k\dfrac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{d}^{2}}}$
Where coulomb’s constant$(k)=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$
Charge density $(\lambda )=\dfrac{totalch\arg e}{length}$ .
Properties of magnetic lines of force are:
Magnetic line density reduces as the distance between the poles increases
Magnetic field lines start from the North Pole and end at the South Pole.
Magnetic lines will not intersect with one another.
Two magnetic lines of force cannot intersect each other because if two magnetic field lines intersect there will be two directions of magnetic field at that point which is impossible.
Flux coming out of the cube is:
${{\phi }_{c}}=\dfrac{\lambda \cdot a\sqrt{3}}{{{\varepsilon }_{0}}}$ $\cdots \cdots (1)$
Flux coming out of the sphere is:
${{\phi }_{s}}=\dfrac{\lambda \cdot 20}{{{\varepsilon }_{0}}}$ $\cdots \cdots (2)$
Dividing equation (1) by (2) then we get
$\dfrac{{{\phi }_{c}}}{{{\phi }_{s}}}=\dfrac{\sqrt{3}}{2}$
So the correct option is C.

Note:Student’s the gravitational forces are always attractive while the electrostatic forces are either attractive or repulsive. The magnitude of electric field is obtained by coulomb’s law and in case of a unit stationary point charge coulomb’s law derivation formula is similar to gauss law derivation. The space around a charge is always under stress and experiences a force on another charge when placed there. The region or space in which stress exists is called the electric field (or dielectric or electrostatic) field.