Question

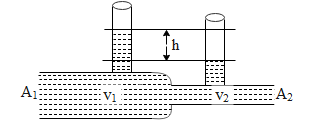
A liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross sections, ${{\text{A}}_{\text{1}}}$ and ${{\text{A}}_{\text{2}}}$ are ${{\text{v}}_{\text{1}}}$ and ${{\text{v}}_{\text{2}}}$ respectively. The difference in the level of the liquid in the two vertical tubes is h. Then

a) The volume of the liquid flowing through the tube in unit time is ${{A}_{1}}{{v}_{1}}$
b) ${{v}_{2}}-{{v}_{1}}=\sqrt{2gh}$
c) ${{v}_{2}}^{2}-{{v}_{1}}^{2}=2gh$
d) The energy per unit mass of the liquid is same in both the tubes

Answer 1

Hint: In the above figure the liquid flows with two different velocities across two different cross sectional areas. Hence there is a difference in pressure across the two regions indicated by the height h in the above figure. The above question is a MCQ question with more than one answer. Using Bernoulli's theorem and equation of continuity, let us verify the conditions mentioned in the options and accordingly determine which one of them holds true.

Complete step by step answer:
To begin with let us first define the equation of continuity and Bernoulli’s theorem.
Equation of continuity: It states that during the streamlined flow of the non viscous and incompressible fluid through a pipe of varying cross section, the product of the area of cross section and the normal fluid velocity remains constant.
Bernoulli’s theorem: It states that the sum of the pressure, kinetic energy and the potential energy per unit volume of an incompressible, non viscous fluid in a streamlined irrational flow remains constant along a streamlined.
From the above equation of continuity we can say that ${{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}=\text{constant}$, where \[{{A}_{1}}\] is the cross sectional area of the tube where in the fluid flows with velocity \[{{v}_{1}}\] and \[{{A}_{2}}\] is the cross sectional area of the tube where in the fluid flows with velocity \[{{v}_{2}}\]. Hence the amount of the liquid flowing through given volume is the same across two different cross sectional areas. From this we can conclude that option a is valid.
If we consider Bernoulli's theorem it is basically based on conservation of energy, which says that the sum of the potential and the kinetic energy per unit volume remains constant. The density of the liquid does not change when it enters from one tube to another tube. Hence the energy per unit mass remains constant. From this as well we can conclude that option d also holds true.
The Bernoulli’s theorem can be mathematically written as,
$P+\dfrac{1}{2}\rho {{v}^{2}}=\text{constant}...\text{(1)}$ where P is the pressure of the fluid, $\rho $is the density of the fluid and v is the velocity of the fluid in motion. In the above scenario the fluid moves across two different cross sections, hence the equation 1 can be written as,
${{P}_{1}}+\dfrac{1}{2}\rho {{v}_{1}}^{2}={{P}_{2}}+\dfrac{1}{2}\rho {{v}_{2}}^{2}=\text{constant}$
${{P}_{1}}-{{P}_{2}}+=\dfrac{1}{2}\rho {{v}_{2}}^{2}-\dfrac{1}{2}\rho {{v}_{1}}^{2}$ the difference in pressure of the fluid i.e. ${{P}_{1}}-{{P}_{2}}=\rho gh$ where g is acceleration due to gravity and h is the height of the difference in water column of the liquid as shown in the above diagram. Hence the above equation can be written as,
$\begin{align}
  & \rho gh=\dfrac{1}{2}\rho ({{v}_{2}}^{2}-{{v}_{1}}^{2}) \\
 & 2gh=({{v}_{2}}^{2}-{{v}_{1}}^{2}) \\
\end{align}$
From the above result we can conclude that option c is also correct.

So, the correct answers are “Option A, C and D”.

Note: Bernoulli’s equation is only applicable to incompressible fluids because it does not take into account the elastic energy of the fluids. Bernoulli's principle does not take into account the angular momentum of the fluid. Hence it cannot be applied to the fluids flowing in curved paths.