
A long horizontal mirror is next to a vertical screen (see figure). Parallel light rays are falling on the mirror at an angle
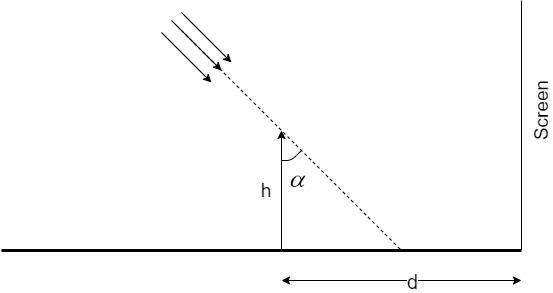
A.
B.
C.
D.
Answer
143.7k+ views
Hint: To solve this problem, we have to understand two important concepts and apply them in our problem:
i) Law of reflection: The incident angle is equal to the reflected angle.
ii) The trigonometric ratio,
Complete step by step answer:
The law of reflection states that the incident angle is equal to the reflected angle.
The object of height h is placed on the mirror. The shadow of the object falls on the mirror and the same shadow is reflected back on the screen
The corresponding geometry for the same is given in this figure:
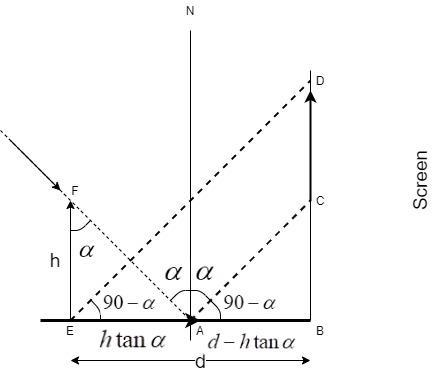
Let us understand the formation of the above geometry in detail.
When the object shadow falls on the mirror at the points A and E, it undergoes a reflection on the plane mirror and an image CD is formed on the screen.
At point A, we have a normal N. The angle made by the ray FA is equal to
At point A, the incident angle is equal to
Since N is the normal, the angle NAB being equal to 90, the angle CAB =
Since AC is parallel to ED,
In the triangle AEF,
Thus,
Given that, AE + AB = d
To calculate the length of the shadow, we need to consider two triangles ABC and EBD to calculate the value of the length CD which is our required value.
In triangle ABC,
The trigonometrical identity equal to
Hence,
In triangle EBD,
The trigonometrical identity equal to
Hence,
By equating the values of
The required length,
Substituting the value of CD and the value of
Since
Thus,
Hence, the length of the shadow on the screen, CD = h
Hence, the correct option is Option C.
Note: In this answer, the concept of alternate and corresponding angles are directly applied here. Let us briefly understand them.
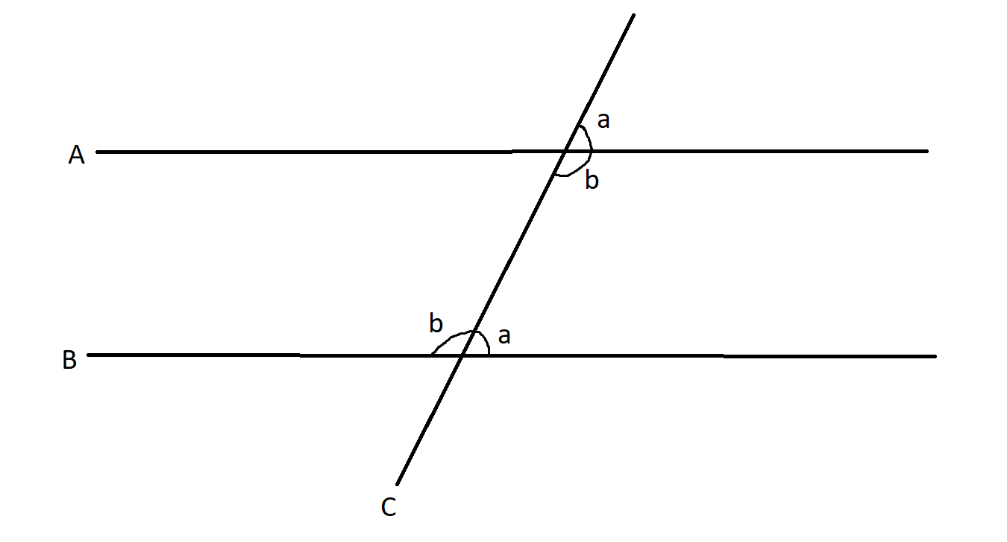
A and B are two parallel lines and the line C which intercepts them at an angle is called the transverse line. When a transverse line intercepts the parallel lines, we get several sets of angles.
Here, angles a are called corresponding angle pair and angles b are called alternate angle pair. The relation between them is
ii) The trigonometric ratio,
Complete step by step answer:
The law of reflection states that the incident angle is equal to the reflected angle.
The object of height h is placed on the mirror. The shadow of the object falls on the mirror and the same shadow is reflected back on the screen
The corresponding geometry for the same is given in this figure:

Let us understand the formation of the above geometry in detail.
When the object shadow falls on the mirror at the points A and E, it undergoes a reflection on the plane mirror and an image CD is formed on the screen.
At point A, we have a normal N. The angle made by the ray FA is equal to
At point A, the incident angle is equal to
Since N is the normal, the angle NAB being equal to 90, the angle CAB =
Since AC is parallel to ED,
In the triangle AEF,
Thus,
Given that, AE + AB = d
To calculate the length of the shadow, we need to consider two triangles ABC and EBD to calculate the value of the length CD which is our required value.
In triangle ABC,
The trigonometrical identity equal to
Hence,
In triangle EBD,
The trigonometrical identity equal to
Hence,
By equating the values of
The required length,
Substituting the value of CD and the value of
Since
Thus,
Hence, the length of the shadow on the screen, CD = h
Hence, the correct option is Option C.
Note: In this answer, the concept of alternate and corresponding angles are directly applied here. Let us briefly understand them.

A and B are two parallel lines and the line C which intercepts them at an angle is called the transverse line. When a transverse line intercepts the parallel lines, we get several sets of angles.
Here, angles a are called corresponding angle pair and angles b are called alternate angle pair. The relation between them is
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
EMI starts from ₹3,487.34 per month
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Physics Average Value and RMS Value JEE Main 2025

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




