Question

A magnetic field (B), uniform between two magnets can be determined measuring the induced voltage in the loop as it is pulled through the gap at a uniform velocity of 20m/s. Size of the magnet is \[2\times 1\times 2cm\] and the size of the coil is \[4\times 6cm\] as shown in figure.

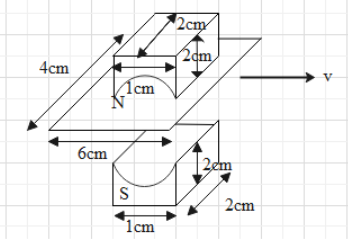
Find the correct variation of induced emf with time. (Assume at time\[t=0\], the coil enters the field.)

Answer 1

Hint: Here a uniform magnetic field is produced by two magnets and a loop is pulled through the gap at uniform velocity of 20m/s, for this set-up we have to find the variation of the induced emf with time. So we will find the induced emf for a particular time period and then plot a graph between the induced emf and time to show its variation.
Formula used:
\[\begin{align}
  & \text{time=}\dfrac{\text{displacement}}{\text{velocity}} \\
 & \varepsilon =-Blv \\
\end{align}\]

Complete Answer:
First we will calculate the time interval which can be measured by using following formula
\[\text{time=}\dfrac{\text{displacement}}{\text{velocity}}\]
At time \[t=0\], loop starts entering the field. When loop covers the distance of 1cm which is the width of the magnets with velocity of 20m/s the time will be given as

\[\begin{align}
  & t=\dfrac{0.01m}{20m/s} \\
 & \Rightarrow t=0.0005s \\
 & \Rightarrow t=500\mu s \\
\end{align}\]
For this time interval the induced emf will be given as
\[\varepsilon =Blv\]
Here B is a magnetic field, l will be the length of the magnets \[\left( l=2cm=0.02m \right)\]and v is the velocity with which the loop is entering. Hence induced emf for time period 0s to 500μs will be
\[\begin{align}
  & \varepsilon =B\left( 0.02 \right)\left( 20 \right) \\
 & \varepsilon =0.4B \\
\end{align}\]
If we consider displacement in steps of 1cm which is the width of magnet then for \[x=2cm\text{ to }x=4cm\] there will be no magnetic field as the loop is totally in between the magnets. Therefore, there won’t be an induced emf.
For \[x=5cm\]that is when the loops covers the distance of 5cm or passed 5cm of its breadth with velocity 20m/s , time will be
\[\begin{align}
  & t=\dfrac{0.05m}{20m/s} \\
 & \Rightarrow t=0.0025s \\
 & \Rightarrow t=2500\mu s \\
\end{align}\]
For \[x=6cm\]that is when loop left the field completely while moving with velocity 20m/s, time will be given as
\[\begin{align}
  & t=\dfrac{0.06m}{20m/s} \\
 & \Rightarrow t=0.0030s \\
 & \Rightarrow t=3000\mu s \\
\end{align}\]

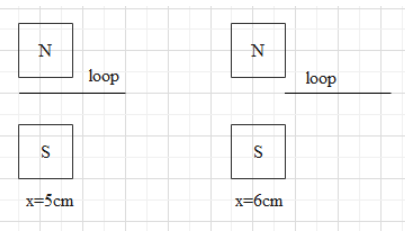
The induced emf for the time interval \[t=2500\mu s\text{ to }t=3000\mu s\]is given as
\[\varepsilon =Blv\]
The negative sign is removed as the loop is leaving the magnetic field velocity will be taken negative and we know negative plus negative is positive. Therefore there won’t be any negative sign.
The length and velocity will be same, hence induced emf becomes
\[\varepsilon =0.4B\]
Now the graph between induced emf and time is given as

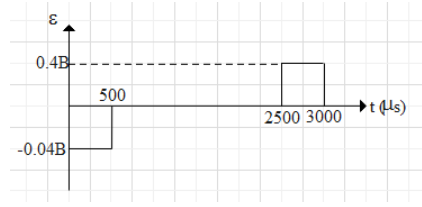
The above graph shows the variation of induced emf with time.

Note:
The graph for the variation of induced emf with time will be the same only time range will change. And induced emf will be –Blv and +Blv. The equation used for induced emf is only for uniform magnetic fields when the magnetic field is perpendicular to velocity. Here epsilon is used to denote emf whereas in the electric field it is used to denote permittivity.